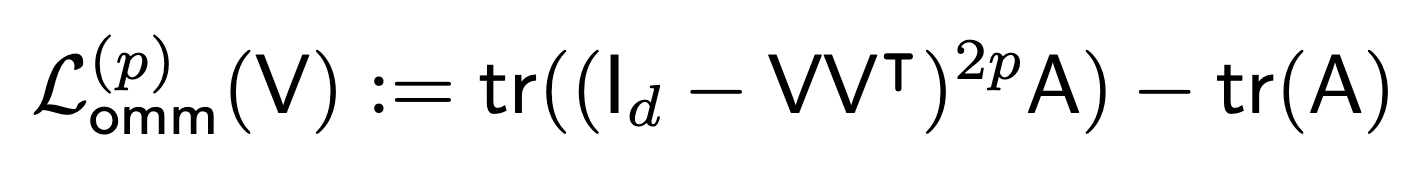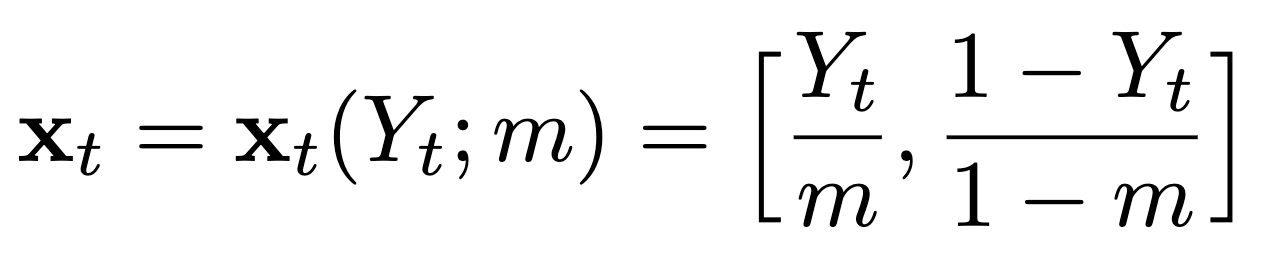publications
Publications in reverse chronological order.
note: * indicates equal contributions. † indicates that the author ordering is alphabetical.
filter by subtopic:
2026
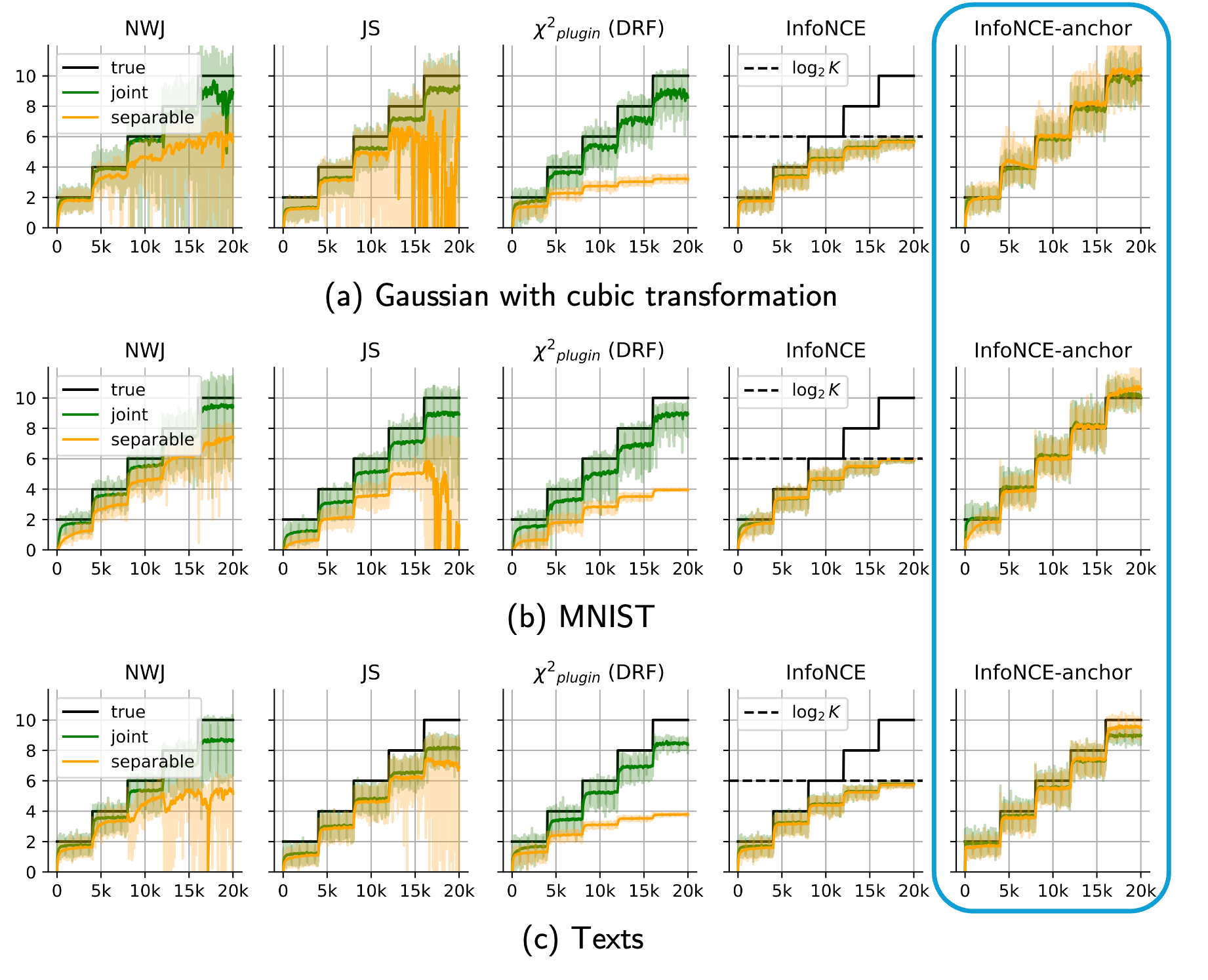
- Contrastive Predictive Coding Done Right for Mutual Information EstimationJ. Jon Ryu, Pavan Yeddanapudi, Xiangxiang Xu, and Gregory W. WornellIn ICLR, April 2026To appear.TL;DR: We show that InfoNCE is an inconsistent MI estimator, and introduce a minimal modification that enables consistent density-ratio estimation and accurate MI estimation.Abs arXiv HTML
The InfoNCE objective, originally introduced for contrastive representation learning, has become a popular choice for mutual information (MI) estimation, despite its indirect connection to MI. In this paper, we demonstrate why InfoNCE should not be regarded as a valid MI estimator, and we introduce a simple modification, which we refer to as InfoNCE-anchor, for accurate MI estimation. Our modification introduces an auxiliary anchor class, enabling consistent density ratio estimation and yielding a plug-in MI estimator with significantly reduced bias. Beyond this, we generalize our framework using proper scoring rules, which recover InfoNCE-anchor as a special case when the log score is employed. This formulation unifies a broad spectrum of contrastive objectives, including NCE, InfoNCE, and f-divergence variants, under a single principled framework. Empirically, we find that InfoNCE-anchor with the log score achieves the most accurate MI estimates; however, in self-supervised representation learning experiments, we find that the anchor does not improve the downstream task performance. These findings corroborate that contrastive representation learning benefits not from accurate MI estimation per se, but from the learning of structured density ratios.
2025
- A Unified View on Learning Unnormalized Distributions via Noise-Contrastive EstimationJ. Jon Ryu, Abhin Shah, and Gregory W. WornellIn ICML, July 2025TL;DR: We provide a unified perspective on various methods for learning unnormalized distributions through the lens of noise-contrastive estimation.Abs arXiv PDF Poster
This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.
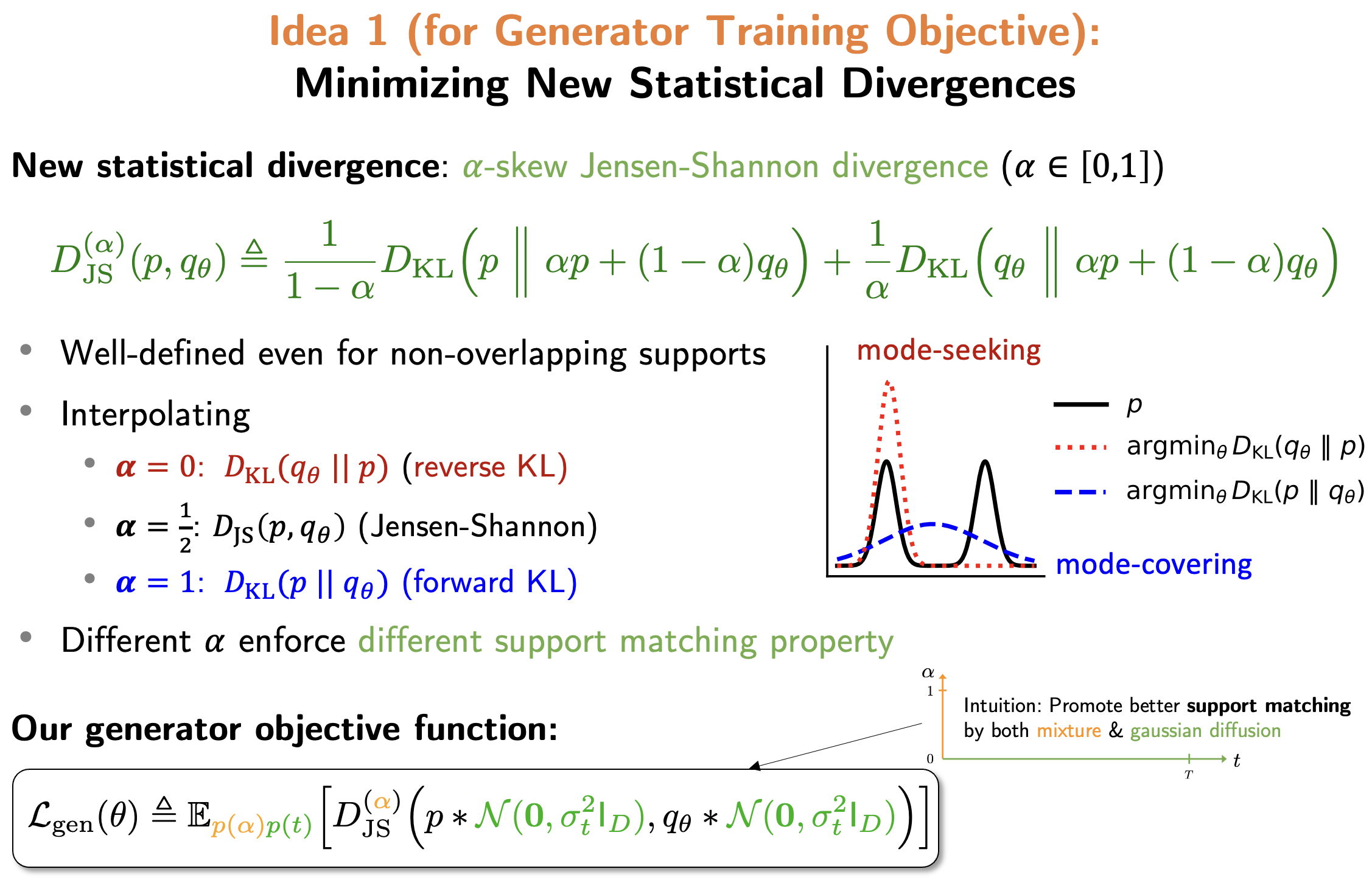
- Score-of-Mixture Training: Training One-Step Generative Models Made SimpleTejas Jayashankar*, J. Jon Ryu*, and Gregory W. WornellIn ICML, July 2025SpotlightTL;DR: We propose a new method for training one-step generative models by minimizing the α-skew Jensen–Shannon divergence using score-based gradient estimates.Abs arXiv PDF Code Poster
Top 2.6% of submissions
We propose Score-of-Mixture Training (SMT), a novel framework for training one-step generative models by minimizing a class of divergences called the α-skew Jensen-Shannon divergence. At its core, SMT estimates the score of mixture distributions between real and fake samples across multiple noise levels. Similar to consistency models, our approach supports both training from scratch (SMT) and distillation using a pretrained diffusion model, which we call Score-of-Mixture Distillation (SMD). It is simple to implement, requires minimal hyperparameter tuning, and ensures stable training. Experiments on CIFAR-10 and ImageNet 64x64 show that SMT/SMD are competitive with and can even outperform existing methods.
- Improved Offline Contextual Bandits with Second-Order Bounds: Betting and FreezingJ. Jon Ryu, Jeongyeol Kwon, Benjamin Koppe, and Kwang-Sung JunIn COLT, June 2025TL;DR: We introduce a betting-based confidence bound for off-policy selection, and a new off-policy learning technique that provides a favorable bias-variance tradeoff.Abs arXiv PDF Code
We consider off-policy selection and learning in contextual bandits, where the learner aims to select or train a reward-maximizing policy using data collected by a fixed behavior policy. Our contribution is two-fold. First, we propose a novel off-policy selection method that leverages a new betting-based confidence bound applied to an inverse propensity weight sequence. Our theoretical analysis reveals that this method achieves a significantly improved, variance-adaptive guarantee over prior work. Second, we propose a novel and generic condition on the optimization objective for off-policy learning that strikes a different balance between bias and variance. One special case, which we call freezing, tends to induce low variance, which is preferred in small-data regimes. Our analysis shows that it matches the best existing guarantees. In our empirical study, our selection method outperforms existing methods, and freezing exhibits improved performance in small-sample regimes.
- Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical SystemsIn NeurIPS, December 2025TL;DR: We show that NeuralSVD (NestedLoRA) provides a scalable and stable approach for learning top-k Koopman singular functions, avoiding the unstable SVD- and inversion-based steps required by VAMPnet/DPNet.Abs arXiv HTML PDF Code Poster
The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.
- Revisiting Orbital Minimization Method for Neural Operator DecompositionJ. Jon Ryu, Samuel Zhou, and Gregory W. WornellIn NeurIPS, December 2025TL;DR: We revisit OMM through a modern lens, developing a scalable NestedOMM formulation that trains neural networks to decompose positive semidefinite operators.Abs arXiv HTML PDF Code Poster
Spectral decomposition of linear operators plays a central role in many areas of machine learning and scientific computing. Recent work has explored training neural networks to approximate eigenfunctions of such operators, enabling scalable approaches to representation learning, dynamical systems, and partial differential equations (PDEs). In this paper, we revisit a classical optimization framework from the computational physics literature known as the *orbital minimization method* (OMM), originally proposed in the 1990s for solving eigenvalue problems in computational chemistry. We provide a simple linear algebraic proof of the consistency of the OMM objective, and reveal connections between this method and several ideas that have appeared independently across different domains. Our primary goal is to justify its broader applicability in modern learning pipelines. We adapt this framework to train neural networks to decompose positive semidefinite operators, and demonstrate its practical advantages across a range of benchmark tasks. Our results highlight how revisiting classical numerical methods through the lens of modern theory and computation can provide not only a principled approach for deploying neural networks in numerical analysis, but also effective and scalable tools for machine learning.
- Alignment as Distribution Learning: Your Preference Model is Explicitly a Language ModelJihun Yun, Juno Kim, Jongho Park, Junhyuck Kim, J. Jon Ryu, Jaewoong Cho, and Kwang-Sung JunJune 2025TL;DR: We recast alignment as distribution learning from preferences, deriving three objectives with O(1/n) convergence to the target LM and without the degeneracy issues of RLHF/DPO.Abs arXiv
Alignment via reinforcement learning from human feedback (RLHF) has become the dominant paradigm for controlling the quality of outputs from large language models (LLMs). However, when viewed as ‘loss + regularization,’ the standard RLHF objective lacks theoretical justification and incentivizes degenerate, deterministic solutions, an issue that variants such as Direct Policy Optimization (DPO) also inherit. In this paper, we rethink alignment by framing it as distribution learning from pairwise preference feedback by explicitly modeling how information about the target language model bleeds through the preference data. This explicit modeling leads us to propose three principled learning objectives: preference maximum likelihood estimation, preference distillation, and reverse KL minimization. We theoretically show that all three approaches enjoy strong non-asymptotic O(1/n) convergence to the target language model, naturally avoiding degeneracy and reward overfitting. Finally, we empirically demonstrate that our distribution learning framework, especially preference distillation, consistently outperforms or matches the performances of RLHF and DPO across various tasks and models.
2024
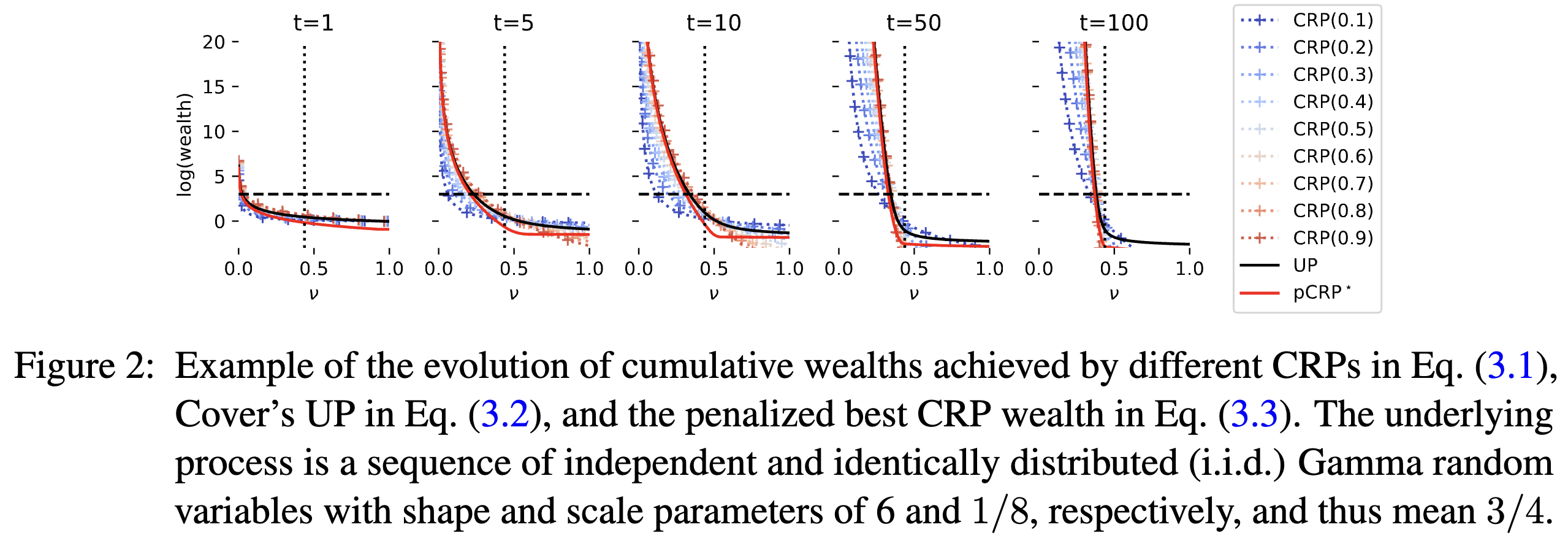
- On Confidence Sequences for Bounded Random Processes via Universal Gambling StrategiesJ. Jon Ryu and Alankrita BhattIEEE TransIT, June 2024TL;DR: We provide a simple two-horse-race perspective for constructing confidence sequences for bounded random processes, demonstrate new properties of the confidence sequence induced by universal portfolio, and propose its computationally efficient relaxations.Abs arXiv HTML PDF Code
This paper considers the problem of constructing a confidence sequence, which is a sequence of confidence intervals that hold uniformly over time, for estimating the mean of bounded real-valued random processes. This paper revisits the gambling-based approach established in the recent literature from a natural \emphtwo-horse race perspective, and demonstrates new properties of the resulting algorithm induced by Cover (1991)’s universal portfolio. The main result of this paper is a new algorithm based on a mixture of lower bounds, which closely approximates the performance of Cover’s universal portfolio with constant per-round time complexity. A higher-order generalization of a lower bound on a logarithmic function in (Fan et al., 2015), which is developed as a key technique for the proposed algorithm, may be of independent interest.
- ISIT
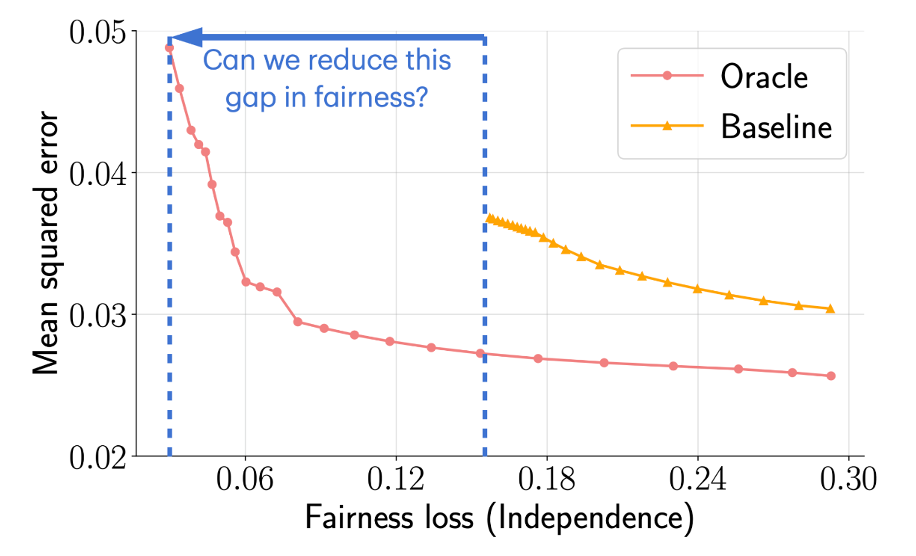 Group Fairness with Uncertainty in Sensitive AttributesAbhin Shah, Maohao Shen, J. Jon Ryu, Subhro Das, Prasanna Sattigeri, Yuheng Bu, and Gregory W. WornellIn ISIT, July 2024A preliminary version of this manuscript was presented at ICML 2023 Workshop on Spurious Correlations, Invariance, and Stability.TL;DR: We propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes.Abs arXiv PDF
Group Fairness with Uncertainty in Sensitive AttributesAbhin Shah, Maohao Shen, J. Jon Ryu, Subhro Das, Prasanna Sattigeri, Yuheng Bu, and Gregory W. WornellIn ISIT, July 2024A preliminary version of this manuscript was presented at ICML 2023 Workshop on Spurious Correlations, Invariance, and Stability.TL;DR: We propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes.Abs arXiv PDFLearning a fair predictive model is crucial to mitigate biased decisions against minority groups in high-stakes applications. A common approach to learn such a model involves solving an optimization problem that maximizes the predictive power of the model under an appropriate group fairness constraint. However, in practice, sensitive attributes are often missing or noisy resulting in uncertainty. We demonstrate that solely enforcing fairness constraints on uncertain sensitive attributes can fall significantly short in achieving the level of fairness of models trained without uncertainty. To overcome this limitation, we propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes. The algorithm is guided by a Gaussian analysis for the independence notion of fairness where we propose a robust quadratically constrained quadratic problem to ensure a strict fairness guarantee with uncertain sensitive attributes. Our algorithm is applicable to both discrete and continuous sensitive attributes and is effective in real-world classification and regression tasks for various group fairness notions, e.g., independence and separation.
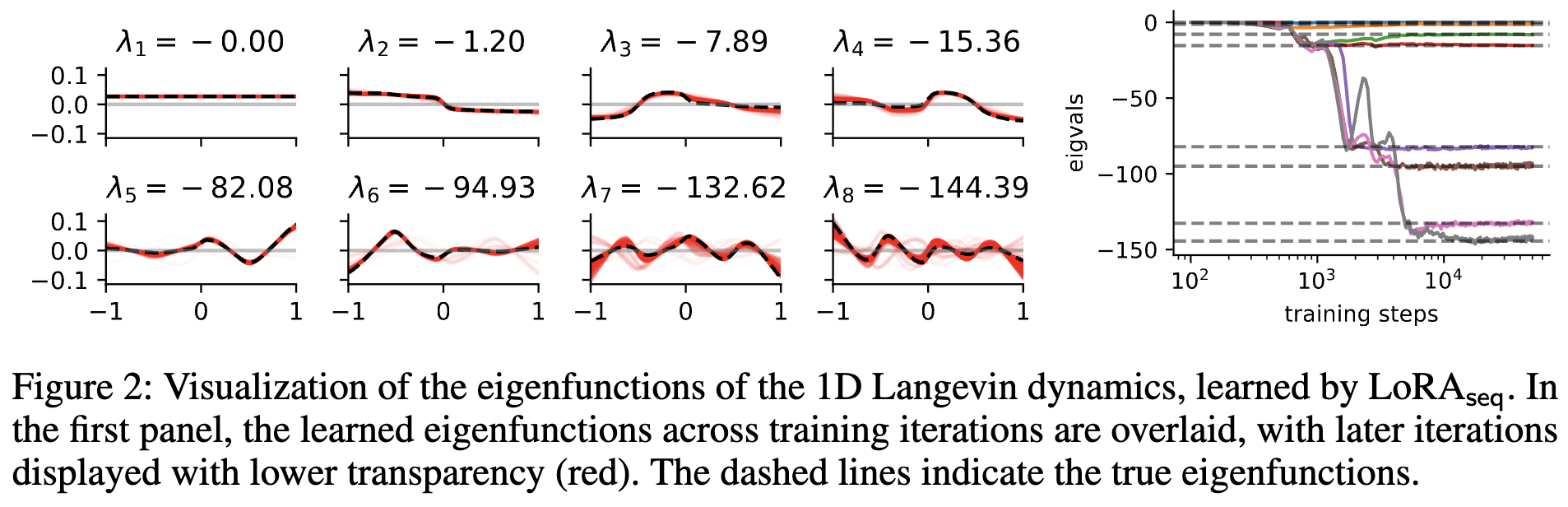
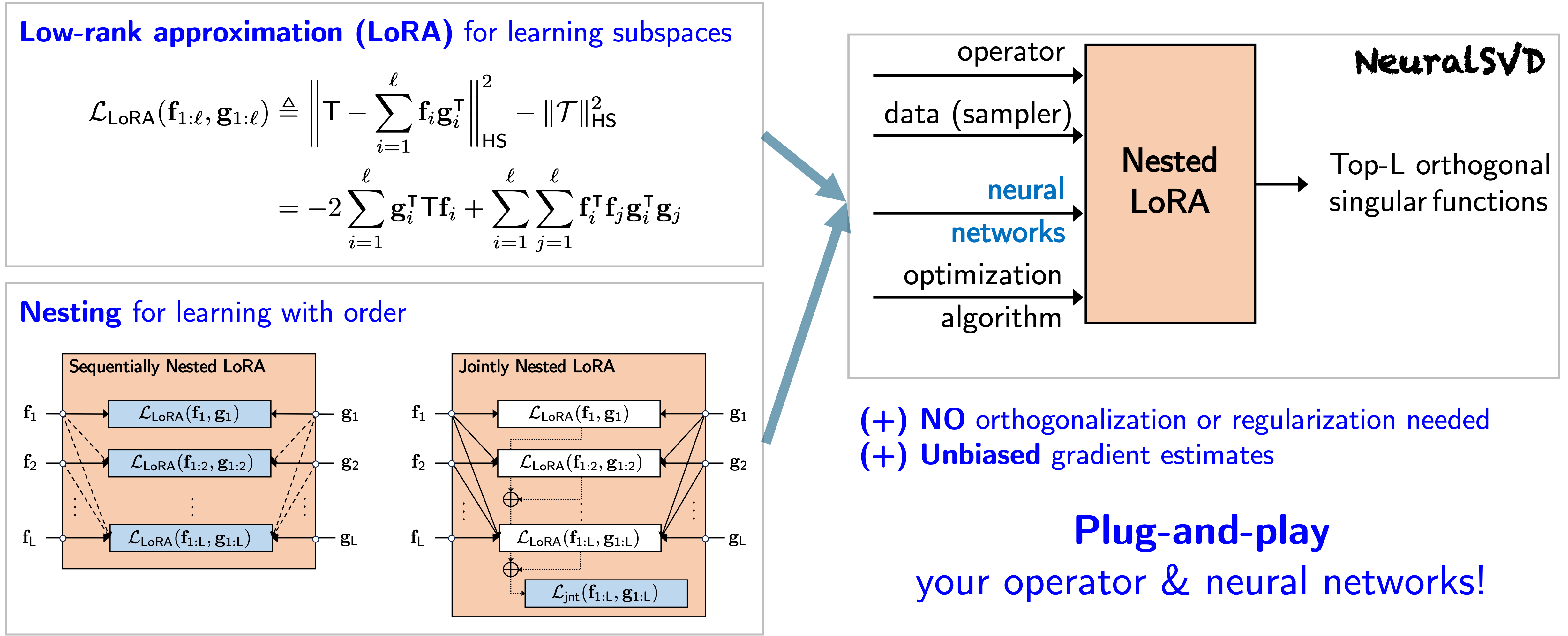
- Operator SVD with Neural Networks via Nested Low-Rank ApproximationIn ICML, July 2024An extended abstract was presented at Machine Learning and the Physical Sciences Workshop, NeurIPS 2023.TL;DR: We propose an efficient unconstrained nested optimization framework for computing the leading singular values and singular functions of a linear operator using neural networks.Abs arXiv HTML PDF Code Poster Slides
Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-L singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.
- Gambling-Based Confidence Sequences for Bounded Random VectorsJ. Jon Ryu and Gregory W. WornellIn ICML, July 2024SpotlightTL;DR: We propose a new approach to constructing confidence sequences for means of bounded multivariate stochastic processes using a general gambling framework.Abs arXiv HTML PDF Code Poster
Top 3.5% of submissions
A confidence sequence (CS) is a sequence of confidence sets that contains a target parameter of an underlying stochastic process at any time step with high probability. This paper proposes a new approach to constructing CSs for means of bounded multivariate stochastic processes using a general gambling framework, extending the recently established coin toss framework for bounded random processes. The proposed gambling framework provides a general recipe for constructing CSs for categorical and probability-vector-valued observations, as well as for general bounded multidimensional observations through a simple reduction. This paper specifically explores the use of the mixture portfolio, akin to Cover’s universal portfolio, in the proposed framework and investigates the properties of the resulting CSs. Simulations demonstrate the tightness of these confidence sequences compared to existing methods. When applied to the sampling without-replacement setting for finite categorical data, it is shown that the resulting CS based on a universal gambling strategy is provably tighter than that of the posterior-prior ratio martingale proposed by Waudby-Smith and Ramdas.
- Are Uncertainty Quantification Capabilities of Evidential Deep Learning a Mirage?Maohao Shen*, J. Jon Ryu*, Soumya Ghosh, Yuheng Bu, Prasanna Sattigeri, Subhro Das, and Gregory W. WornellIn NeurIPS, December 2024TL;DR: We theoretically characterize the pitfalls of evidential deep learning (EDL) in quantifying predictive uncertainty by unifying various EDL objective functions, and empirically demonstrate their failure modes.Abs arXiv HTML PDF Code Poster Slides
This paper questions the effectiveness of a modern predictive uncertainty quantification approach, called \emphevidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their perceived strong empirical performance on downstream tasks, a line of recent studies by Bengs et al. identify limitations of the existing methods to conclude their learned epistemic uncertainties are unreliable, e.g., in that they are non-vanishing even with infinite data. Building on and sharpening such analysis, we 1) provide a sharper understanding of the asymptotic behavior of a wide class of EDL methods by unifying various objective functions; 2) reveal that the EDL methods can be better interpreted as an out-of-distribution detection algorithm based on energy-based-models; and 3) conduct extensive ablation studies to better assess their empirical effectiveness with real-world datasets. Through all these analyses, we conclude that even when EDL methods are empirically effective on downstream tasks, this occurs despite their poor uncertainty quantification capabilities. Our investigation suggests that incorporating model uncertainty can help EDL methods faithfully quantify uncertainties and further improve performance on representative downstream tasks, albeit at the cost of additional computational complexity.
- Tech. ReportLifted Residual Score EstimationDecember 2024An extended abstract was presented at ICML 2024 Workshop on Structured Probabilistic Inference & Generative Modeling.TL;DR: We propose lifted score estimation and residual score estimation, two complementary techniques that together improve score learning across VAEs, WAEs, and diffusion models.Abs
This paper proposes two new techniques to improve the accuracy of score estimation. The first proposal is a new objective function called the \emphlifted score estimation objective, which serves as a replacement for the score matching (SM) objective. Instead of minimizing the expected \ell_2^2-distance between the learned and true score models, the proposed objective operates in the \emphlifted space of the outer-product of a vector-valued function with itself. The distance is defined as the expected squared Frobenius norm of the difference between such matrix-valued objects induced by the learned and true score functions. The second idea is to model and learn the \emphresidual approximation error of the learned score estimator, given a base score model architecture. We empirically demonstrate that the combination of the two ideas called \emphlifted residual score estimation outperforms sliced SM in training VAE and WAE with implicit encoders, and denoising SM in training diffusion models, as evaluated by downstream metrics of sample quality such as the FID score.
2023
- On Universal Portfolios with Continuous Side InformationAlankrita Bhatt*, J. Jon Ryu*, and Young-Han KimIn AISTATS, April 2023TL;DR: We propose a universal portfolio strategy that adapts to a continuous side-information sequence.Abs arXiv HTML PDF
A new portfolio selection strategy that adapts to a continuous side-information sequence is presented, with a universal wealth guarantee against a class of state-constant rebalanced portfolios with respect to a state function that maps each side-information symbol to a finite set of states. In particular, given that a state function belongs to a collection of functions of finite Natarajan dimension, the proposed strategy is shown to achieve, asymptotically to first order in the exponent, the same wealth as the best state-constant rebalanced portfolio with respect to the best state function, chosen in hindsight from observed market. This result can be viewed as an extension of the seminal work of Cover and Ordentlich (1996) that assumes a single state function.
2022
- Nearest neighbor density functional estimation from inverse Laplace transformIEEE TransIT, February 2022TL;DR: We propose a general recipe to design a L_2-consistent estimator for general density functionals (such as KL divergence) based on k-nearest neighbors.Abs arXiv HTML PDF Code Slides
A new approach to L_2-consistent estimation of a general density functional using k-nearest neighbor distances is proposed, where the functional under consideration is in the form of the expectation of some function f of the densities at each point. The estimator is designed to be asymptotically unbiased, using the convergence of the normalized volume of a k-nearest neighbor ball to a Gamma distribution in the large-sample limit, and naturally involves the inverse Laplace transform of a scaled version of the function f. Some instantiations of the proposed estimator recover existing k-nearest neighbor based estimators of Shannon and Rényi entropies and Kullback-Leibler and Rényi divergences, and discover new consistent estimators for many other functionals such as logarithmic entropies and divergences. The L_2-consistency of the proposed estimator is established for a broad class of densities for general functionals, and the convergence rate in mean squared error is established as a function of the sample size for smooth, bounded densities.
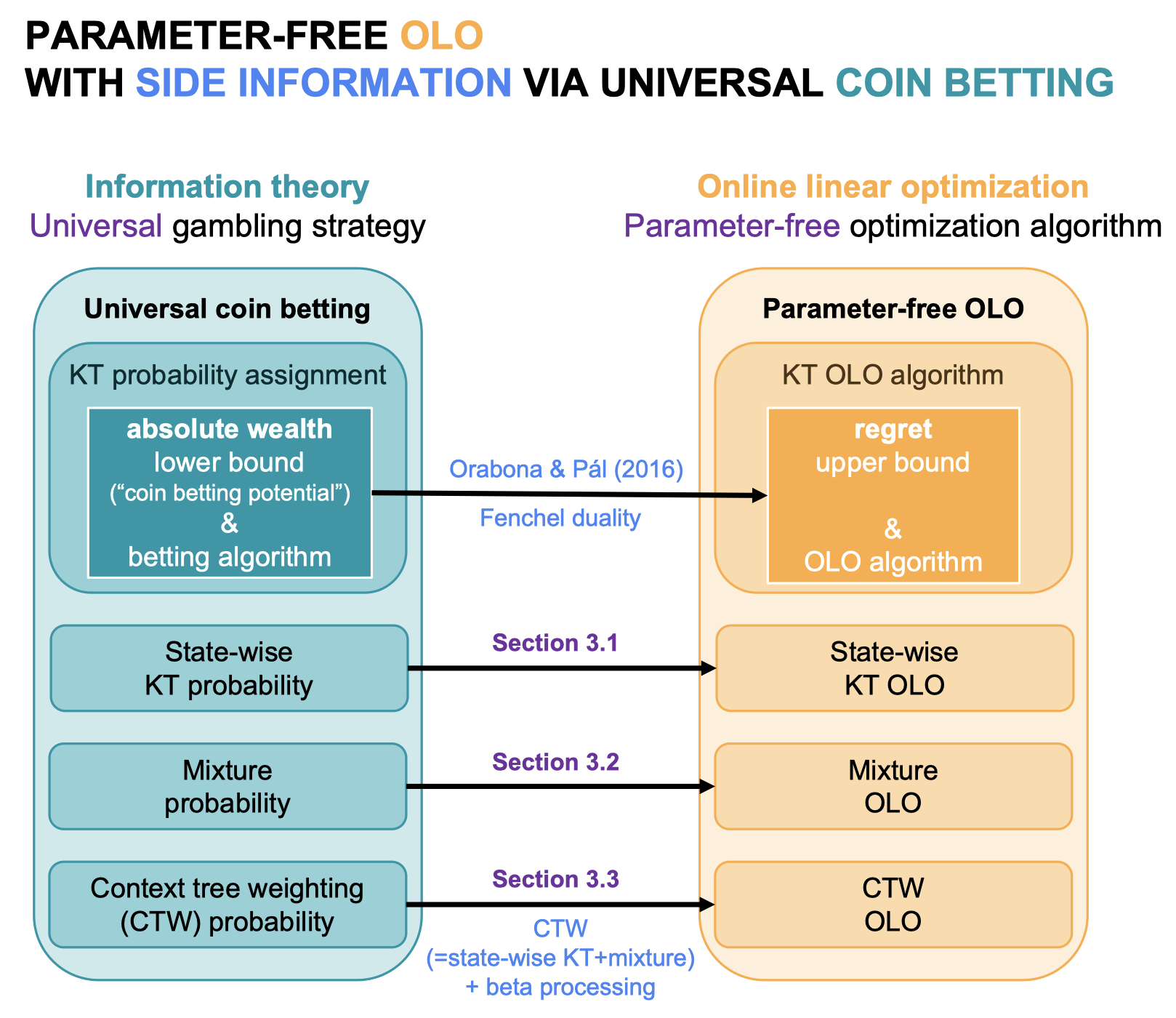
- Parameter-Free Online Linear Optimization with Side Information via Universal Coin BettingJ. Jon Ryu, Alankrita Bhatt, and Young-Han KimIn AISTATS, March 2022TL;DR: We propose a parameter-free online linear optimization algorithm that adapts to **tree-structured side information**.Abs arXiv HTML PDF Code Poster Slides
A class of parameter-free online linear optimization algorithms is proposed that harnesses the structure of an adversarial sequence by adapting to some side information. These algorithms combine the reduction technique of Orabona and Pál (2016) for adapting coin betting algorithms for online linear optimization with universal compression techniques in information theory for incorporating sequential side information to coin betting. Concrete examples are studied in which the side information has a tree structure and consists of quantized values of the previous symbols of the adversarial sequence, including fixed-order and variable-order Markov cases. By modifying the context-tree weighting technique of Willems, Shtarkov, and Tjalkens (1995), the proposed algorithm is further refined to achieve the best performance over all adaptive algorithms with tree-structured side information of a given maximum order in a computationally efficient manner.
- PhD thesisFrom Information Theory to Machine Learning Algorithms: A Few VignettesJongha Jon RyuUniversity of California San Diego, September 2022
This dissertation illustrates how certain information-theoretic ideas and views on learning problems can lead to new algorithms via concrete examples.The three information-theoretic strategies taken in this dissertation are (1) to abstract out the gist of a learning problem in the infinite-sample limit; (2) to reduce a learning problem into a probability estimation problem and plugging-in a "good" probability; and (3) to adapt and apply relevant results from information theory. These are applied to three topics in machine learning, including representation learning, nearest-neighbor methods, and universal information processing, where two problems are studied from each topic.
- Minimax Optimal Algorithms with Fixed-k-Nearest NeighborsJ. Jon Ryu and Young-Han KimSeptember 2022TL;DR: We present how to perform minimax optimal classification, regression, and density estimation based on small-k nearest neighbor (NN) searches.Abs arXiv Code
This paper presents how to perform minimax optimal classification, regression, and density estimation based on fixed-k nearest neighbor (NN) searches. We consider a distributed learning scenario, in which a massive dataset is split into smaller groups, where the k-NNs are found for a query point with respect to each subset of data. We propose \emphoptimal rules to aggregate the fixed-k-NN information for classification, regression, and density estimation that achieve minimax optimal rates for the respective problems. We show that the distributed algorithm with a fixed k over a sufficiently large number of groups attains a minimax optimal error rate up to a multiplicative logarithmic factor under some regularity conditions. Roughly speaking, distributed k-NN rules with M groups has a performance comparable to the standard Θ(kM)-NN rules even for fixed k.
- Learning with Succinct Common Representation with Wyner’s Common InformationSeptember 2022Preliminary versions were presented at the Bayesian Deep Learning Workshop at NeurIPS 2018 and at the Bayesian Deep Learning workshop at NeurIPS 2021.TL;DR: We propose a bimodal generative model that operationalizes Wyner’s common information by learning a succinct shared representation for joint and conditional generation.Abs arXiv Code Slides
A new bimodal generative model is proposed for generating conditional and joint samples, accompanied with a training method with learning a succinct bottleneck representation. The proposed model, dubbed as the variational Wyner model, is designed based on two classical problems in network information theory—distributed simulation and channel synthesis—in which Wyner’s common information arises as the fundamental limit on the succinctness of the common representation. The model is trained by minimizing the symmetric Kullback–Leibler divergence between variational and model distributions with regularization terms for common information, reconstruction consistency, and latent space matching terms, which is carried out via an adversarial density ratio estimation technique. The utility of the proposed approach is demonstrated through experiments for joint and conditional generation with synthetic and real-world datasets, as well as a challenging zero-shot image retrieval task.
- An Information-Theoretic Proof of Kac–Bernstein TheoremJ. Jon Ryu and Young-Han KimSeptember 2022TL;DR: We give a short information-theoretic proof of the Kac–Bernstein characterization of the normal distribution.Abs arXiv
A short, information-theoretic proof of the Kac–Bernstein theorem, which is stated as follows, is presented: For any independent random variables X and Y, if X+Y and X-Y are independent, then X and Y are normally distributed.
2021
- ISIT
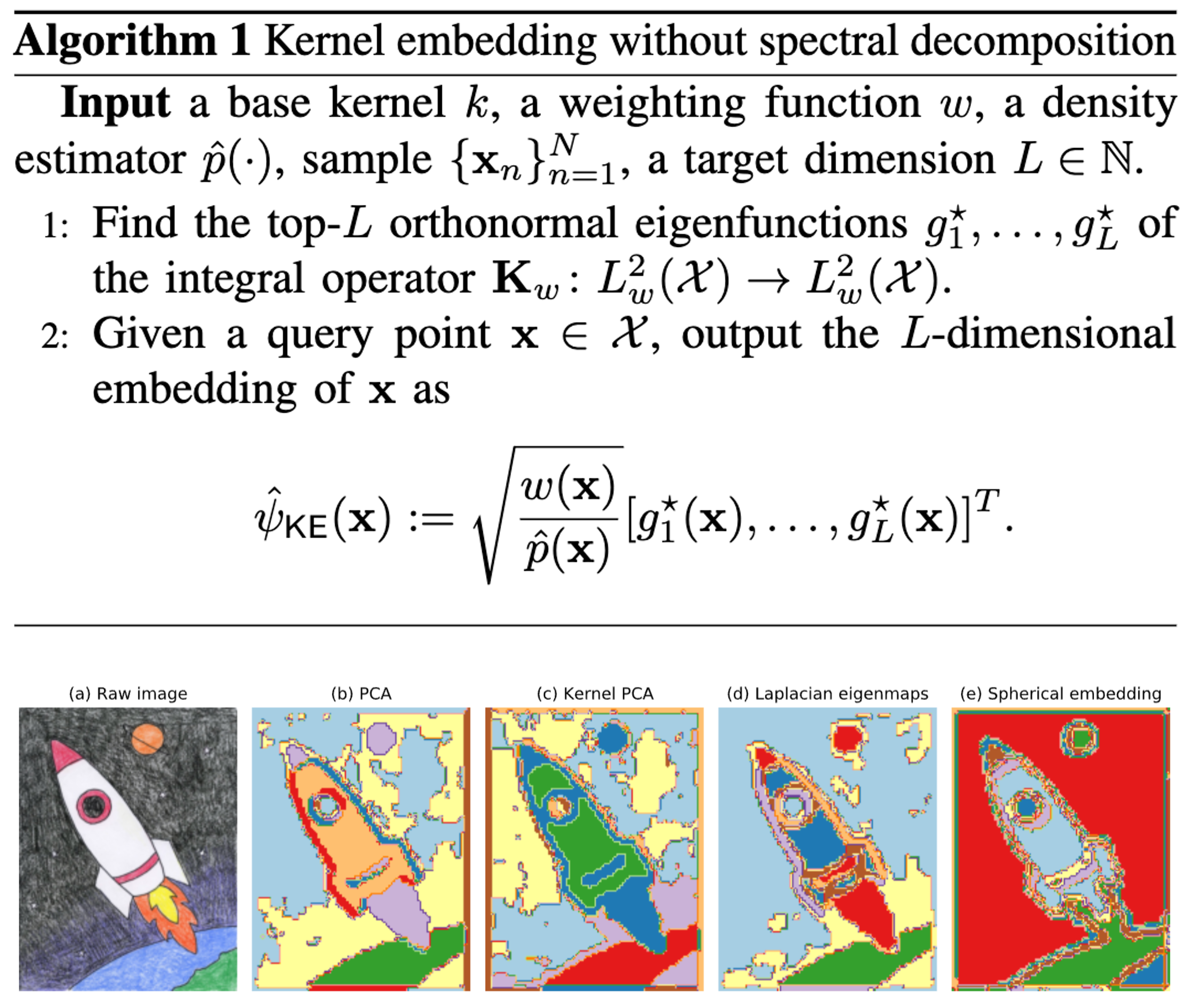 On the Role of Eigendecomposition in Kernel EmbeddingJ. Jon Ryu, Jiun-Ting Huang, and Young-Han KimIn ISIT, September 2021TL;DR: We propose an eigendecomposition-free kernel embedding method that only requires density estimation at query points.Abs HTML PDF Slides
On the Role of Eigendecomposition in Kernel EmbeddingJ. Jon Ryu, Jiun-Ting Huang, and Young-Han KimIn ISIT, September 2021TL;DR: We propose an eigendecomposition-free kernel embedding method that only requires density estimation at query points.Abs HTML PDF SlidesThis paper proposes a special variant of Laplacian eigenmaps, whose solution is characterized by the underlying density and the eigenfunctions of the associated Hilbert–Schmidt operator of a similarity kernel function. In contrast to existing kernel-based spectral methods such as kernel principal component analysis and Laplacian eigenmaps, the new embedding algorithm only involves estimating density at each query point without any eigendecomposition of a matrix. A concrete example of dot-product kernels over hypersphere is provided to illustrate the applicability of the proposed framework.
2020
- ICASSP
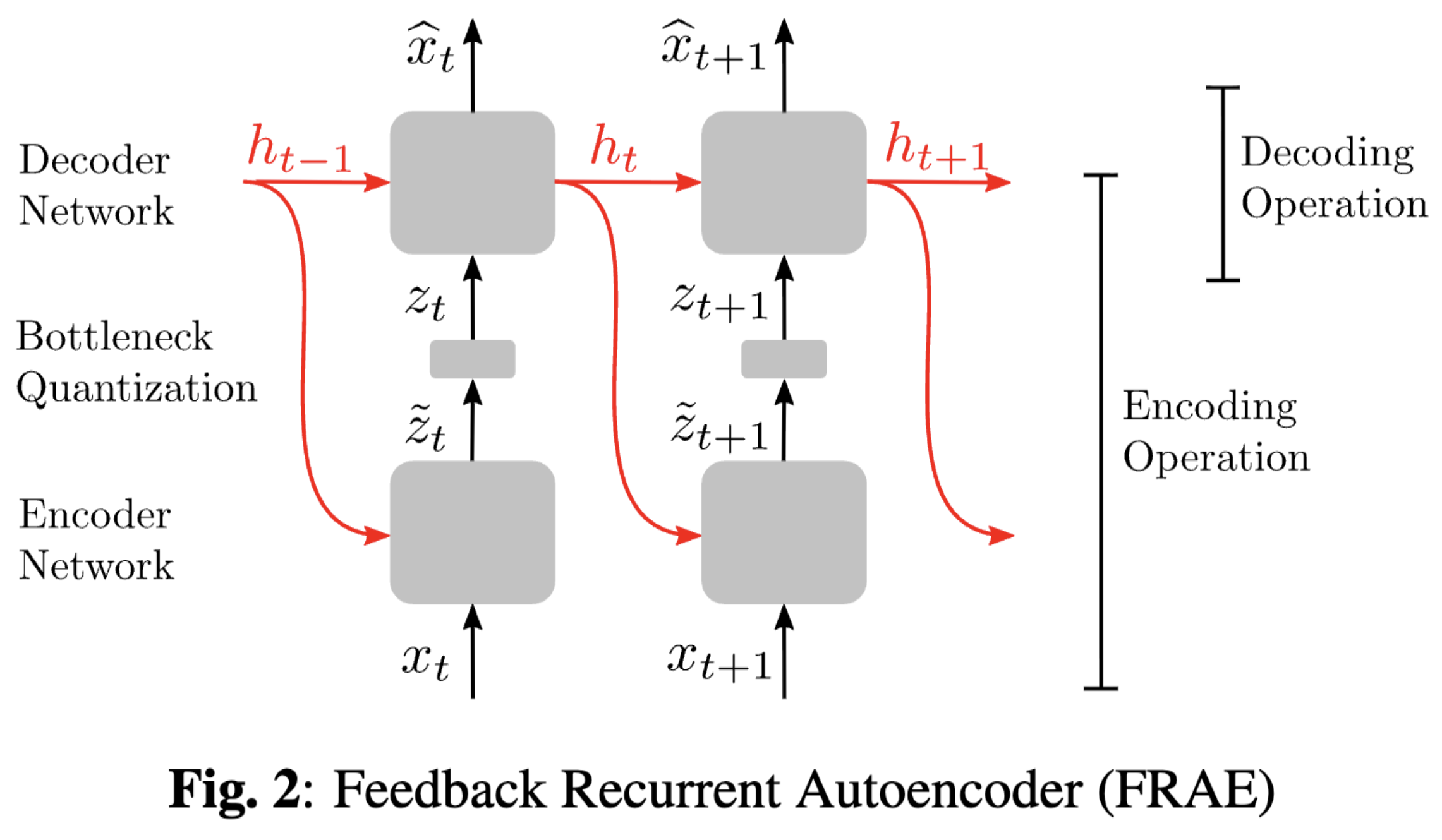 Feedback Recurrent AutoencoderYang Yang, Guillaume Sautière, J. Jon Ryu, and Taco S. CohenIn Proc. IEEE Int. Conf. Acoust. Speech Signal Process. (ICASSP), September 2020TL;DR: We propose a new recurrent autoencoder architecture for online compression of sequential data with temporal dependency.Abs arXiv HTML PDF
Feedback Recurrent AutoencoderYang Yang, Guillaume Sautière, J. Jon Ryu, and Taco S. CohenIn Proc. IEEE Int. Conf. Acoust. Speech Signal Process. (ICASSP), September 2020TL;DR: We propose a new recurrent autoencoder architecture for online compression of sequential data with temporal dependency.Abs arXiv HTML PDFIn this work, we propose a new recurrent autoencoder architecture, termed Feedback Recurrent AutoEncoder (FRAE), for online compression of sequential data with temporal dependency. The recurrent structure of FRAE is designed to efficiently extract the redundancy along the time dimension and allows a compact discrete representation of the data to be learned. We demonstrate its effectiveness in speech spectrogram compression. Specifically, we show that the FRAE, paired with a powerful neural vocoder, can produce high-quality speech waveforms at a low, fixed bitrate. We further show that by adding a learned prior for the latent space and using an entropy coder, we can achieve an even lower variable bitrate.
2018
- ICIP
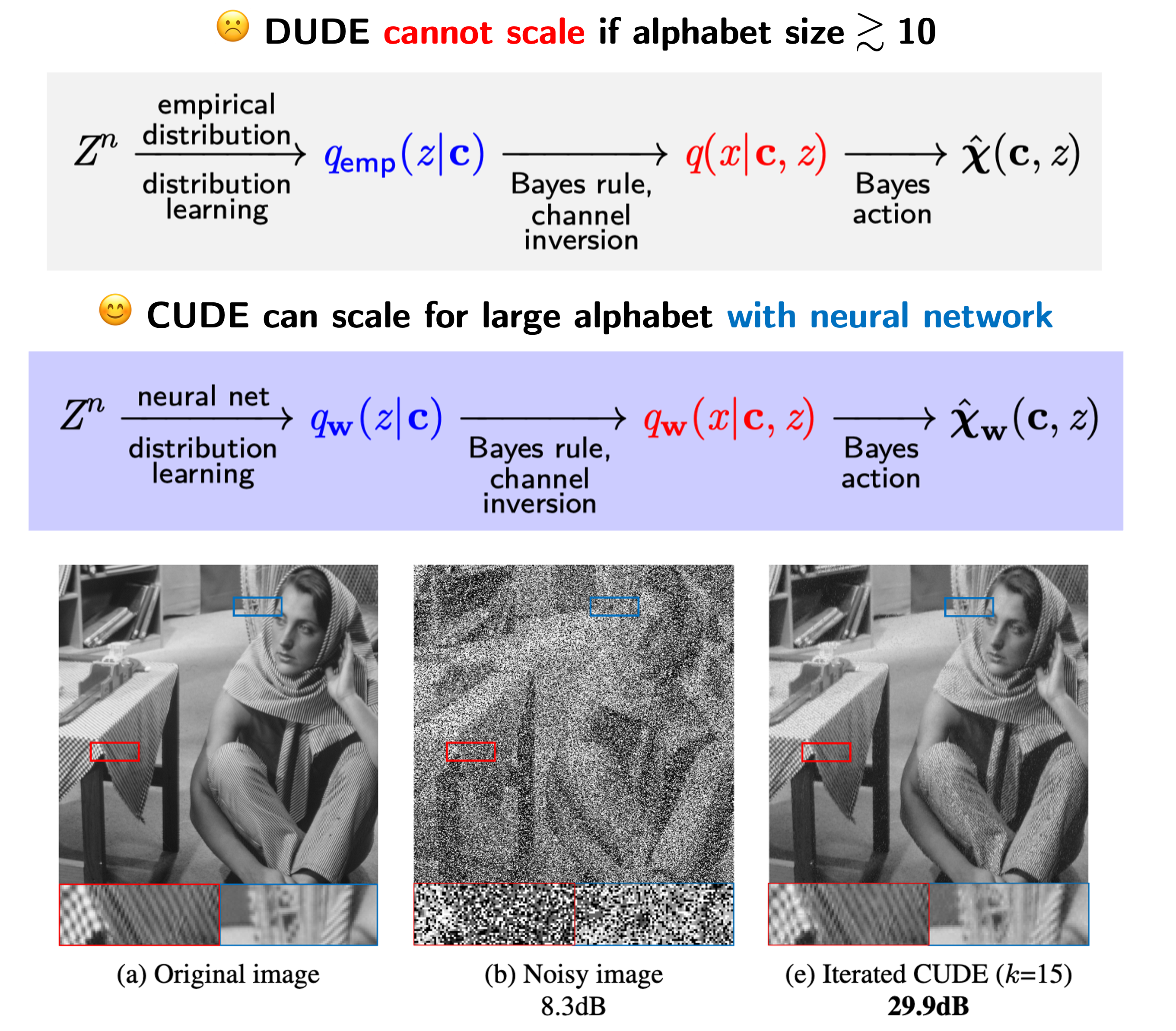 Conditional distribution learning with neural networks and its application to universal image denoisingJongha Ryu and Young-Han KimIn Proc. IEEE Int. Conf. Image Proc. (ICIP), September 2018TL;DR: We extend a simple deep-learning-extension of the information-theoretic universal denoising algorithm DUDE for structured, large-alphabet problems such as image denoising.Abs HTML PDF Poster Slides
Conditional distribution learning with neural networks and its application to universal image denoisingJongha Ryu and Young-Han KimIn Proc. IEEE Int. Conf. Image Proc. (ICIP), September 2018TL;DR: We extend a simple deep-learning-extension of the information-theoretic universal denoising algorithm DUDE for structured, large-alphabet problems such as image denoising.Abs HTML PDF Poster SlidesA simple and scalable denoising algorithm is proposed that can be applied to a wide range of source and noise models. At the core of the proposed CUDE algorithm is symbol-by-symbol universal denoising used by the celebrated DUDE algorithm, whereby the optimal estimate of the source from an unknown distribution is computed by inverting the empirical distribution of the noisy observation sequence by a deep neural network, which naturally and implicitly aggregates multi-pie contexts of similar characteristics and estimates the conditional distribution more accurately. The performance of CUDE is evaluated for grayscale images of varying bit depths, which improves upon DUDE and its recent neural network based extension, Neural DUDE.
- ITW
 Variations on a theme by Liu, Cuff, and Verdú: The power of posterior samplingIn ITW, September 2018TL;DR: We explore the power of multiple random guesses in statistical inference.Abs HTML PDF Slides
Variations on a theme by Liu, Cuff, and Verdú: The power of posterior samplingIn ITW, September 2018TL;DR: We explore the power of multiple random guesses in statistical inference.Abs HTML PDF SlidesThe Liu–Cuff–Verdu lemma states that in estimating a source X from an observation Y, making a random guess X’ from the posterior p(x|y) can go wrong at most twice as often as the optimal answer. Several variations of this fundamental, yet rather arcane, result are explored for detection, decoding, and estimation problems.
- Allerton
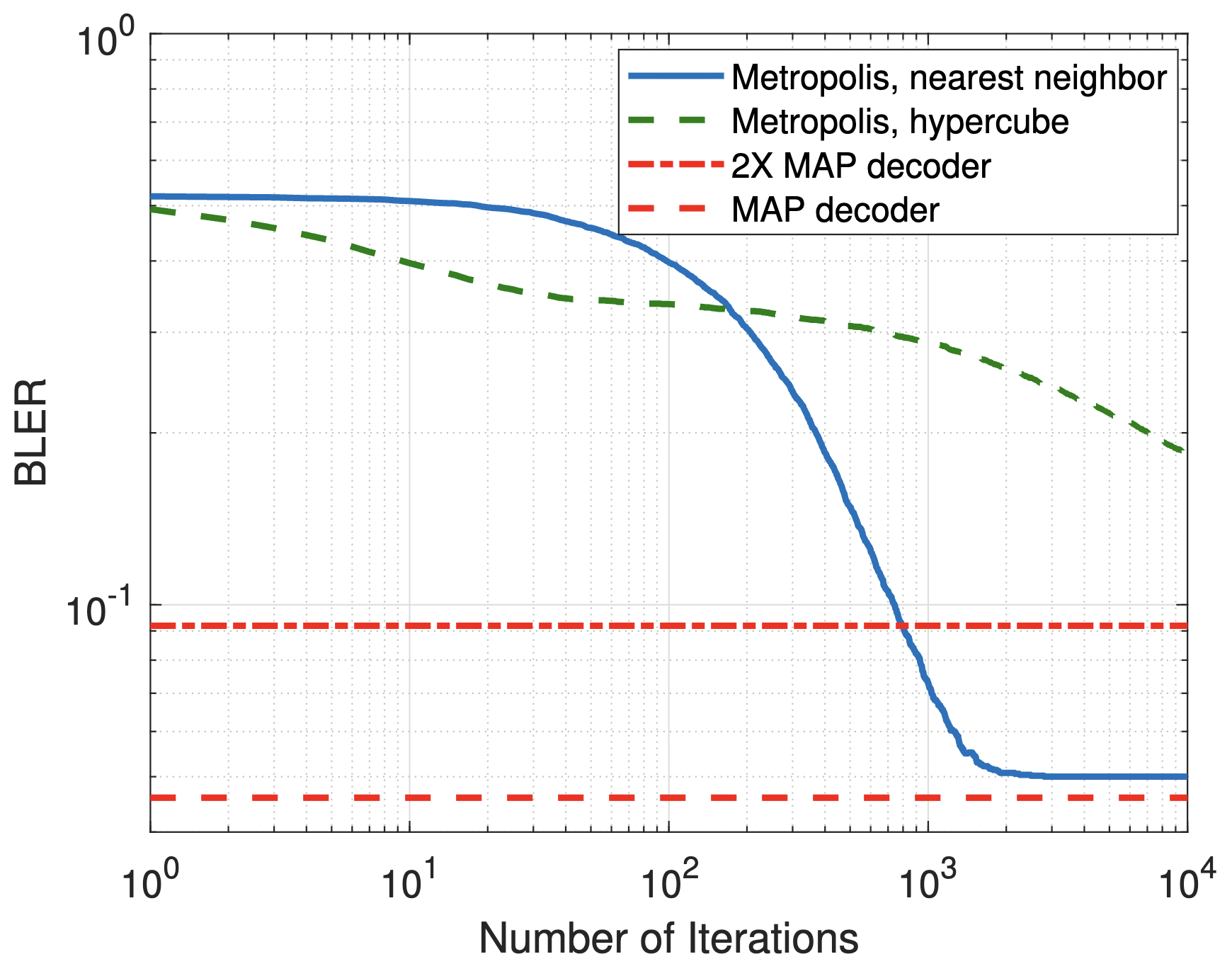 Monte Carlo methods for randomized likelihood decodingIn Allerton, September 2018TL;DR: We explore the potential of randomized decoding based on sampling from the posterior distribution via Monte Carlo techniques.Abs HTML PDF
Monte Carlo methods for randomized likelihood decodingIn Allerton, September 2018TL;DR: We explore the potential of randomized decoding based on sampling from the posterior distribution via Monte Carlo techniques.Abs HTML PDFA randomized decoder that generates the message estimate according to the posterior distribution is known to achieve the reliability comparable to that of the maximum a posteriori probability decoder. With a goal of practical implementations of such a randomized decoder, several Monte Carlo techniques, such as rejection sampling, Gibbs sampling, and the Metropolis algorithm, are adapted to the problem of efficient sampling from the posterior distribution. Analytical and experimental results compare the complexity and performance of these Monte Carlo decoders for simple linear codes and the binary symmetric channel.
2017
- Energy-based sequence GANs for recommendation and their connection to imitation learningJaeyoon Yoo, Heonseok Ha, Jihun Yi, Jongha Ryu, Chanju Kim, Jung-Woo Ha, Young-Han Kim, and Sungroh YoonSeptember 2017TL;DR: We reinterpret EB-SeqGANs for recommendation as maximum-entropy imitation learning by viewing the energy function as a feature function.Abs arXiv
Recommender systems aim to find an accurate and efficient mapping from historic data of user-preferred items to a new item that is to be liked by a user. Towards this goal, energy-based sequence generative adversarial nets (EB-SeqGANs) are adopted for recommendation by learning a generative model for the time series of user-preferred items. By recasting the energy function as the feature function, the proposed EB-SeqGANs is interpreted as an instance of maximum-entropy imitation learning.
Preprints
2025
- Alignment as Distribution Learning: Your Preference Model is Explicitly a Language ModelJihun Yun, Juno Kim, Jongho Park, Junhyuck Kim, J. Jon Ryu, Jaewoong Cho, and Kwang-Sung JunJune 2025TL;DR: We recast alignment as distribution learning from preferences, deriving three objectives with O(1/n) convergence to the target LM and without the degeneracy issues of RLHF/DPO.Abs arXiv
Alignment via reinforcement learning from human feedback (RLHF) has become the dominant paradigm for controlling the quality of outputs from large language models (LLMs). However, when viewed as ‘loss + regularization,’ the standard RLHF objective lacks theoretical justification and incentivizes degenerate, deterministic solutions, an issue that variants such as Direct Policy Optimization (DPO) also inherit. In this paper, we rethink alignment by framing it as distribution learning from pairwise preference feedback by explicitly modeling how information about the target language model bleeds through the preference data. This explicit modeling leads us to propose three principled learning objectives: preference maximum likelihood estimation, preference distillation, and reverse KL minimization. We theoretically show that all three approaches enjoy strong non-asymptotic O(1/n) convergence to the target language model, naturally avoiding degeneracy and reward overfitting. Finally, we empirically demonstrate that our distribution learning framework, especially preference distillation, consistently outperforms or matches the performances of RLHF and DPO across various tasks and models.
2022
- Minimax Optimal Algorithms with Fixed-k-Nearest NeighborsJ. Jon Ryu and Young-Han KimJune 2022TL;DR: We present how to perform minimax optimal classification, regression, and density estimation based on small-k nearest neighbor (NN) searches.Abs arXiv Code
This paper presents how to perform minimax optimal classification, regression, and density estimation based on fixed-k nearest neighbor (NN) searches. We consider a distributed learning scenario, in which a massive dataset is split into smaller groups, where the k-NNs are found for a query point with respect to each subset of data. We propose \emphoptimal rules to aggregate the fixed-k-NN information for classification, regression, and density estimation that achieve minimax optimal rates for the respective problems. We show that the distributed algorithm with a fixed k over a sufficiently large number of groups attains a minimax optimal error rate up to a multiplicative logarithmic factor under some regularity conditions. Roughly speaking, distributed k-NN rules with M groups has a performance comparable to the standard Θ(kM)-NN rules even for fixed k.
- Learning with Succinct Common Representation with Wyner’s Common InformationJune 2022Preliminary versions were presented at the Bayesian Deep Learning Workshop at NeurIPS 2018 and at the Bayesian Deep Learning workshop at NeurIPS 2021.TL;DR: We propose a bimodal generative model that operationalizes Wyner’s common information by learning a succinct shared representation for joint and conditional generation.Abs arXiv Code Slides
A new bimodal generative model is proposed for generating conditional and joint samples, accompanied with a training method with learning a succinct bottleneck representation. The proposed model, dubbed as the variational Wyner model, is designed based on two classical problems in network information theory—distributed simulation and channel synthesis—in which Wyner’s common information arises as the fundamental limit on the succinctness of the common representation. The model is trained by minimizing the symmetric Kullback–Leibler divergence between variational and model distributions with regularization terms for common information, reconstruction consistency, and latent space matching terms, which is carried out via an adversarial density ratio estimation technique. The utility of the proposed approach is demonstrated through experiments for joint and conditional generation with synthetic and real-world datasets, as well as a challenging zero-shot image retrieval task.
Journal articles
2024
- On Confidence Sequences for Bounded Random Processes via Universal Gambling StrategiesJ. Jon Ryu and Alankrita BhattIEEE TransIT, June 2024TL;DR: We provide a simple two-horse-race perspective for constructing confidence sequences for bounded random processes, demonstrate new properties of the confidence sequence induced by universal portfolio, and propose its computationally efficient relaxations.Abs arXiv HTML PDF Code
This paper considers the problem of constructing a confidence sequence, which is a sequence of confidence intervals that hold uniformly over time, for estimating the mean of bounded real-valued random processes. This paper revisits the gambling-based approach established in the recent literature from a natural \emphtwo-horse race perspective, and demonstrates new properties of the resulting algorithm induced by Cover (1991)’s universal portfolio. The main result of this paper is a new algorithm based on a mixture of lower bounds, which closely approximates the performance of Cover’s universal portfolio with constant per-round time complexity. A higher-order generalization of a lower bound on a logarithmic function in (Fan et al., 2015), which is developed as a key technique for the proposed algorithm, may be of independent interest.
2022
- Nearest neighbor density functional estimation from inverse Laplace transformIEEE TransIT, February 2022TL;DR: We propose a general recipe to design a L_2-consistent estimator for general density functionals (such as KL divergence) based on k-nearest neighbors.Abs arXiv HTML PDF Code Slides
A new approach to L_2-consistent estimation of a general density functional using k-nearest neighbor distances is proposed, where the functional under consideration is in the form of the expectation of some function f of the densities at each point. The estimator is designed to be asymptotically unbiased, using the convergence of the normalized volume of a k-nearest neighbor ball to a Gamma distribution in the large-sample limit, and naturally involves the inverse Laplace transform of a scaled version of the function f. Some instantiations of the proposed estimator recover existing k-nearest neighbor based estimators of Shannon and Rényi entropies and Kullback-Leibler and Rényi divergences, and discover new consistent estimators for many other functionals such as logarithmic entropies and divergences. The L_2-consistency of the proposed estimator is established for a broad class of densities for general functionals, and the convergence rate in mean squared error is established as a function of the sample size for smooth, bounded densities.
Conference papers
2026
- Contrastive Predictive Coding Done Right for Mutual Information EstimationJ. Jon Ryu, Pavan Yeddanapudi, Xiangxiang Xu, and Gregory W. WornellIn ICLR, April 2026To appear.TL;DR: We show that InfoNCE is an inconsistent MI estimator, and introduce a minimal modification that enables consistent density-ratio estimation and accurate MI estimation.Abs arXiv HTML
The InfoNCE objective, originally introduced for contrastive representation learning, has become a popular choice for mutual information (MI) estimation, despite its indirect connection to MI. In this paper, we demonstrate why InfoNCE should not be regarded as a valid MI estimator, and we introduce a simple modification, which we refer to as InfoNCE-anchor, for accurate MI estimation. Our modification introduces an auxiliary anchor class, enabling consistent density ratio estimation and yielding a plug-in MI estimator with significantly reduced bias. Beyond this, we generalize our framework using proper scoring rules, which recover InfoNCE-anchor as a special case when the log score is employed. This formulation unifies a broad spectrum of contrastive objectives, including NCE, InfoNCE, and f-divergence variants, under a single principled framework. Empirically, we find that InfoNCE-anchor with the log score achieves the most accurate MI estimates; however, in self-supervised representation learning experiments, we find that the anchor does not improve the downstream task performance. These findings corroborate that contrastive representation learning benefits not from accurate MI estimation per se, but from the learning of structured density ratios.
2025
- A Unified View on Learning Unnormalized Distributions via Noise-Contrastive EstimationJ. Jon Ryu, Abhin Shah, and Gregory W. WornellIn ICML, July 2025TL;DR: We provide a unified perspective on various methods for learning unnormalized distributions through the lens of noise-contrastive estimation.Abs arXiv PDF Poster
This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.
- Score-of-Mixture Training: Training One-Step Generative Models Made SimpleTejas Jayashankar*, J. Jon Ryu*, and Gregory W. WornellIn ICML, July 2025SpotlightTL;DR: We propose a new method for training one-step generative models by minimizing the α-skew Jensen–Shannon divergence using score-based gradient estimates.Abs arXiv PDF Code Poster
Top 2.6% of submissions
We propose Score-of-Mixture Training (SMT), a novel framework for training one-step generative models by minimizing a class of divergences called the α-skew Jensen-Shannon divergence. At its core, SMT estimates the score of mixture distributions between real and fake samples across multiple noise levels. Similar to consistency models, our approach supports both training from scratch (SMT) and distillation using a pretrained diffusion model, which we call Score-of-Mixture Distillation (SMD). It is simple to implement, requires minimal hyperparameter tuning, and ensures stable training. Experiments on CIFAR-10 and ImageNet 64x64 show that SMT/SMD are competitive with and can even outperform existing methods.
- Improved Offline Contextual Bandits with Second-Order Bounds: Betting and FreezingJ. Jon Ryu, Jeongyeol Kwon, Benjamin Koppe, and Kwang-Sung JunIn COLT, June 2025TL;DR: We introduce a betting-based confidence bound for off-policy selection, and a new off-policy learning technique that provides a favorable bias-variance tradeoff.Abs arXiv PDF Code
We consider off-policy selection and learning in contextual bandits, where the learner aims to select or train a reward-maximizing policy using data collected by a fixed behavior policy. Our contribution is two-fold. First, we propose a novel off-policy selection method that leverages a new betting-based confidence bound applied to an inverse propensity weight sequence. Our theoretical analysis reveals that this method achieves a significantly improved, variance-adaptive guarantee over prior work. Second, we propose a novel and generic condition on the optimization objective for off-policy learning that strikes a different balance between bias and variance. One special case, which we call freezing, tends to induce low variance, which is preferred in small-data regimes. Our analysis shows that it matches the best existing guarantees. In our empirical study, our selection method outperforms existing methods, and freezing exhibits improved performance in small-sample regimes.
- Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical SystemsIn NeurIPS, December 2025TL;DR: We show that NeuralSVD (NestedLoRA) provides a scalable and stable approach for learning top-k Koopman singular functions, avoiding the unstable SVD- and inversion-based steps required by VAMPnet/DPNet.Abs arXiv HTML PDF Code Poster
The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.
- Revisiting Orbital Minimization Method for Neural Operator DecompositionJ. Jon Ryu, Samuel Zhou, and Gregory W. WornellIn NeurIPS, December 2025TL;DR: We revisit OMM through a modern lens, developing a scalable NestedOMM formulation that trains neural networks to decompose positive semidefinite operators.Abs arXiv HTML PDF Code Poster
Spectral decomposition of linear operators plays a central role in many areas of machine learning and scientific computing. Recent work has explored training neural networks to approximate eigenfunctions of such operators, enabling scalable approaches to representation learning, dynamical systems, and partial differential equations (PDEs). In this paper, we revisit a classical optimization framework from the computational physics literature known as the *orbital minimization method* (OMM), originally proposed in the 1990s for solving eigenvalue problems in computational chemistry. We provide a simple linear algebraic proof of the consistency of the OMM objective, and reveal connections between this method and several ideas that have appeared independently across different domains. Our primary goal is to justify its broader applicability in modern learning pipelines. We adapt this framework to train neural networks to decompose positive semidefinite operators, and demonstrate its practical advantages across a range of benchmark tasks. Our results highlight how revisiting classical numerical methods through the lens of modern theory and computation can provide not only a principled approach for deploying neural networks in numerical analysis, but also effective and scalable tools for machine learning.
2024
- ISIT
 Group Fairness with Uncertainty in Sensitive AttributesAbhin Shah, Maohao Shen, J. Jon Ryu, Subhro Das, Prasanna Sattigeri, Yuheng Bu, and Gregory W. WornellIn ISIT, July 2024A preliminary version of this manuscript was presented at ICML 2023 Workshop on Spurious Correlations, Invariance, and Stability.TL;DR: We propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes.Abs arXiv PDF
Group Fairness with Uncertainty in Sensitive AttributesAbhin Shah, Maohao Shen, J. Jon Ryu, Subhro Das, Prasanna Sattigeri, Yuheng Bu, and Gregory W. WornellIn ISIT, July 2024A preliminary version of this manuscript was presented at ICML 2023 Workshop on Spurious Correlations, Invariance, and Stability.TL;DR: We propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes.Abs arXiv PDFLearning a fair predictive model is crucial to mitigate biased decisions against minority groups in high-stakes applications. A common approach to learn such a model involves solving an optimization problem that maximizes the predictive power of the model under an appropriate group fairness constraint. However, in practice, sensitive attributes are often missing or noisy resulting in uncertainty. We demonstrate that solely enforcing fairness constraints on uncertain sensitive attributes can fall significantly short in achieving the level of fairness of models trained without uncertainty. To overcome this limitation, we propose a bootstrap-based algorithm that achieves the target level of fairness despite the uncertainty in sensitive attributes. The algorithm is guided by a Gaussian analysis for the independence notion of fairness where we propose a robust quadratically constrained quadratic problem to ensure a strict fairness guarantee with uncertain sensitive attributes. Our algorithm is applicable to both discrete and continuous sensitive attributes and is effective in real-world classification and regression tasks for various group fairness notions, e.g., independence and separation.
- Operator SVD with Neural Networks via Nested Low-Rank ApproximationIn ICML, July 2024An extended abstract was presented at Machine Learning and the Physical Sciences Workshop, NeurIPS 2023.TL;DR: We propose an efficient unconstrained nested optimization framework for computing the leading singular values and singular functions of a linear operator using neural networks.Abs arXiv HTML PDF Code Poster Slides
Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-L singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.
- Gambling-Based Confidence Sequences for Bounded Random VectorsJ. Jon Ryu and Gregory W. WornellIn ICML, July 2024SpotlightTL;DR: We propose a new approach to constructing confidence sequences for means of bounded multivariate stochastic processes using a general gambling framework.Abs arXiv HTML PDF Code Poster
Top 3.5% of submissions
A confidence sequence (CS) is a sequence of confidence sets that contains a target parameter of an underlying stochastic process at any time step with high probability. This paper proposes a new approach to constructing CSs for means of bounded multivariate stochastic processes using a general gambling framework, extending the recently established coin toss framework for bounded random processes. The proposed gambling framework provides a general recipe for constructing CSs for categorical and probability-vector-valued observations, as well as for general bounded multidimensional observations through a simple reduction. This paper specifically explores the use of the mixture portfolio, akin to Cover’s universal portfolio, in the proposed framework and investigates the properties of the resulting CSs. Simulations demonstrate the tightness of these confidence sequences compared to existing methods. When applied to the sampling without-replacement setting for finite categorical data, it is shown that the resulting CS based on a universal gambling strategy is provably tighter than that of the posterior-prior ratio martingale proposed by Waudby-Smith and Ramdas.
- Are Uncertainty Quantification Capabilities of Evidential Deep Learning a Mirage?Maohao Shen*, J. Jon Ryu*, Soumya Ghosh, Yuheng Bu, Prasanna Sattigeri, Subhro Das, and Gregory W. WornellIn NeurIPS, December 2024TL;DR: We theoretically characterize the pitfalls of evidential deep learning (EDL) in quantifying predictive uncertainty by unifying various EDL objective functions, and empirically demonstrate their failure modes.Abs arXiv HTML PDF Code Poster Slides
This paper questions the effectiveness of a modern predictive uncertainty quantification approach, called \emphevidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their perceived strong empirical performance on downstream tasks, a line of recent studies by Bengs et al. identify limitations of the existing methods to conclude their learned epistemic uncertainties are unreliable, e.g., in that they are non-vanishing even with infinite data. Building on and sharpening such analysis, we 1) provide a sharper understanding of the asymptotic behavior of a wide class of EDL methods by unifying various objective functions; 2) reveal that the EDL methods can be better interpreted as an out-of-distribution detection algorithm based on energy-based-models; and 3) conduct extensive ablation studies to better assess their empirical effectiveness with real-world datasets. Through all these analyses, we conclude that even when EDL methods are empirically effective on downstream tasks, this occurs despite their poor uncertainty quantification capabilities. Our investigation suggests that incorporating model uncertainty can help EDL methods faithfully quantify uncertainties and further improve performance on representative downstream tasks, albeit at the cost of additional computational complexity.
2023
- On Universal Portfolios with Continuous Side InformationAlankrita Bhatt*, J. Jon Ryu*, and Young-Han KimIn AISTATS, April 2023TL;DR: We propose a universal portfolio strategy that adapts to a continuous side-information sequence.Abs arXiv HTML PDF
A new portfolio selection strategy that adapts to a continuous side-information sequence is presented, with a universal wealth guarantee against a class of state-constant rebalanced portfolios with respect to a state function that maps each side-information symbol to a finite set of states. In particular, given that a state function belongs to a collection of functions of finite Natarajan dimension, the proposed strategy is shown to achieve, asymptotically to first order in the exponent, the same wealth as the best state-constant rebalanced portfolio with respect to the best state function, chosen in hindsight from observed market. This result can be viewed as an extension of the seminal work of Cover and Ordentlich (1996) that assumes a single state function.
2022
- Parameter-Free Online Linear Optimization with Side Information via Universal Coin BettingJ. Jon Ryu, Alankrita Bhatt, and Young-Han KimIn AISTATS, March 2022TL;DR: We propose a parameter-free online linear optimization algorithm that adapts to **tree-structured side information**.Abs arXiv HTML PDF Code Poster Slides
A class of parameter-free online linear optimization algorithms is proposed that harnesses the structure of an adversarial sequence by adapting to some side information. These algorithms combine the reduction technique of Orabona and Pál (2016) for adapting coin betting algorithms for online linear optimization with universal compression techniques in information theory for incorporating sequential side information to coin betting. Concrete examples are studied in which the side information has a tree structure and consists of quantized values of the previous symbols of the adversarial sequence, including fixed-order and variable-order Markov cases. By modifying the context-tree weighting technique of Willems, Shtarkov, and Tjalkens (1995), the proposed algorithm is further refined to achieve the best performance over all adaptive algorithms with tree-structured side information of a given maximum order in a computationally efficient manner.
2021
- ISIT
 On the Role of Eigendecomposition in Kernel EmbeddingJ. Jon Ryu, Jiun-Ting Huang, and Young-Han KimIn ISIT, March 2021TL;DR: We propose an eigendecomposition-free kernel embedding method that only requires density estimation at query points.Abs HTML PDF Slides
On the Role of Eigendecomposition in Kernel EmbeddingJ. Jon Ryu, Jiun-Ting Huang, and Young-Han KimIn ISIT, March 2021TL;DR: We propose an eigendecomposition-free kernel embedding method that only requires density estimation at query points.Abs HTML PDF SlidesThis paper proposes a special variant of Laplacian eigenmaps, whose solution is characterized by the underlying density and the eigenfunctions of the associated Hilbert–Schmidt operator of a similarity kernel function. In contrast to existing kernel-based spectral methods such as kernel principal component analysis and Laplacian eigenmaps, the new embedding algorithm only involves estimating density at each query point without any eigendecomposition of a matrix. A concrete example of dot-product kernels over hypersphere is provided to illustrate the applicability of the proposed framework.
2020
- ICASSP
 Feedback Recurrent AutoencoderYang Yang, Guillaume Sautière, J. Jon Ryu, and Taco S. CohenIn Proc. IEEE Int. Conf. Acoust. Speech Signal Process. (ICASSP), March 2020TL;DR: We propose a new recurrent autoencoder architecture for online compression of sequential data with temporal dependency.Abs arXiv HTML PDF
Feedback Recurrent AutoencoderYang Yang, Guillaume Sautière, J. Jon Ryu, and Taco S. CohenIn Proc. IEEE Int. Conf. Acoust. Speech Signal Process. (ICASSP), March 2020TL;DR: We propose a new recurrent autoencoder architecture for online compression of sequential data with temporal dependency.Abs arXiv HTML PDFIn this work, we propose a new recurrent autoencoder architecture, termed Feedback Recurrent AutoEncoder (FRAE), for online compression of sequential data with temporal dependency. The recurrent structure of FRAE is designed to efficiently extract the redundancy along the time dimension and allows a compact discrete representation of the data to be learned. We demonstrate its effectiveness in speech spectrogram compression. Specifically, we show that the FRAE, paired with a powerful neural vocoder, can produce high-quality speech waveforms at a low, fixed bitrate. We further show that by adding a learned prior for the latent space and using an entropy coder, we can achieve an even lower variable bitrate.
2018
- ICIP
 Conditional distribution learning with neural networks and its application to universal image denoisingJongha Ryu and Young-Han KimIn Proc. IEEE Int. Conf. Image Proc. (ICIP), March 2018TL;DR: We extend a simple deep-learning-extension of the information-theoretic universal denoising algorithm DUDE for structured, large-alphabet problems such as image denoising.Abs HTML PDF Poster Slides
Conditional distribution learning with neural networks and its application to universal image denoisingJongha Ryu and Young-Han KimIn Proc. IEEE Int. Conf. Image Proc. (ICIP), March 2018TL;DR: We extend a simple deep-learning-extension of the information-theoretic universal denoising algorithm DUDE for structured, large-alphabet problems such as image denoising.Abs HTML PDF Poster SlidesA simple and scalable denoising algorithm is proposed that can be applied to a wide range of source and noise models. At the core of the proposed CUDE algorithm is symbol-by-symbol universal denoising used by the celebrated DUDE algorithm, whereby the optimal estimate of the source from an unknown distribution is computed by inverting the empirical distribution of the noisy observation sequence by a deep neural network, which naturally and implicitly aggregates multi-pie contexts of similar characteristics and estimates the conditional distribution more accurately. The performance of CUDE is evaluated for grayscale images of varying bit depths, which improves upon DUDE and its recent neural network based extension, Neural DUDE.
- ITW
 Variations on a theme by Liu, Cuff, and Verdú: The power of posterior samplingIn ITW, March 2018TL;DR: We explore the power of multiple random guesses in statistical inference.Abs HTML PDF Slides
Variations on a theme by Liu, Cuff, and Verdú: The power of posterior samplingIn ITW, March 2018TL;DR: We explore the power of multiple random guesses in statistical inference.Abs HTML PDF SlidesThe Liu–Cuff–Verdu lemma states that in estimating a source X from an observation Y, making a random guess X’ from the posterior p(x|y) can go wrong at most twice as often as the optimal answer. Several variations of this fundamental, yet rather arcane, result are explored for detection, decoding, and estimation problems.
- Allerton
 Monte Carlo methods for randomized likelihood decodingIn Allerton, March 2018TL;DR: We explore the potential of randomized decoding based on sampling from the posterior distribution via Monte Carlo techniques.Abs HTML PDF
Monte Carlo methods for randomized likelihood decodingIn Allerton, March 2018TL;DR: We explore the potential of randomized decoding based on sampling from the posterior distribution via Monte Carlo techniques.Abs HTML PDFA randomized decoder that generates the message estimate according to the posterior distribution is known to achieve the reliability comparable to that of the maximum a posteriori probability decoder. With a goal of practical implementations of such a randomized decoder, several Monte Carlo techniques, such as rejection sampling, Gibbs sampling, and the Metropolis algorithm, are adapted to the problem of efficient sampling from the posterior distribution. Analytical and experimental results compare the complexity and performance of these Monte Carlo decoders for simple linear codes and the binary symmetric channel.
Miscellaneous
2024
- Tech. ReportLifted Residual Score EstimationMarch 2024An extended abstract was presented at ICML 2024 Workshop on Structured Probabilistic Inference & Generative Modeling.TL;DR: We propose lifted score estimation and residual score estimation, two complementary techniques that together improve score learning across VAEs, WAEs, and diffusion models.Abs
This paper proposes two new techniques to improve the accuracy of score estimation. The first proposal is a new objective function called the \emphlifted score estimation objective, which serves as a replacement for the score matching (SM) objective. Instead of minimizing the expected \ell_2^2-distance between the learned and true score models, the proposed objective operates in the \emphlifted space of the outer-product of a vector-valued function with itself. The distance is defined as the expected squared Frobenius norm of the difference between such matrix-valued objects induced by the learned and true score functions. The second idea is to model and learn the \emphresidual approximation error of the learned score estimator, given a base score model architecture. We empirically demonstrate that the combination of the two ideas called \emphlifted residual score estimation outperforms sliced SM in training VAE and WAE with implicit encoders, and denoising SM in training diffusion models, as evaluated by downstream metrics of sample quality such as the FID score.
2022
- An Information-Theoretic Proof of Kac–Bernstein TheoremJ. Jon Ryu and Young-Han KimMarch 2022TL;DR: We give a short information-theoretic proof of the Kac–Bernstein characterization of the normal distribution.Abs arXiv
A short, information-theoretic proof of the Kac–Bernstein theorem, which is stated as follows, is presented: For any independent random variables X and Y, if X+Y and X-Y are independent, then X and Y are normally distributed.
2017
- Energy-based sequence GANs for recommendation and their connection to imitation learningJaeyoon Yoo, Heonseok Ha, Jihun Yi, Jongha Ryu, Chanju Kim, Jung-Woo Ha, Young-Han Kim, and Sungroh YoonMarch 2017TL;DR: We reinterpret EB-SeqGANs for recommendation as maximum-entropy imitation learning by viewing the energy function as a feature function.Abs arXiv
Recommender systems aim to find an accurate and efficient mapping from historic data of user-preferred items to a new item that is to be liked by a user. Towards this goal, energy-based sequence generative adversarial nets (EB-SeqGANs) are adopted for recommendation by learning a generative model for the time series of user-preferred items. By recasting the energy function as the feature function, the proposed EB-SeqGANs is interpreted as an instance of maximum-entropy imitation learning.
Theses
2022
- PhD thesisFrom Information Theory to Machine Learning Algorithms: A Few VignettesJongha Jon RyuUniversity of California San Diego, September 2022
This dissertation illustrates how certain information-theoretic ideas and views on learning problems can lead to new algorithms via concrete examples.The three information-theoretic strategies taken in this dissertation are (1) to abstract out the gist of a learning problem in the infinite-sample limit; (2) to reduce a learning problem into a probability estimation problem and plugging-in a "good" probability; and (3) to adapt and apply relevant results from information theory. These are applied to three topics in machine learning, including representation learning, nearest-neighbor methods, and universal information processing, where two problems are studied from each topic.