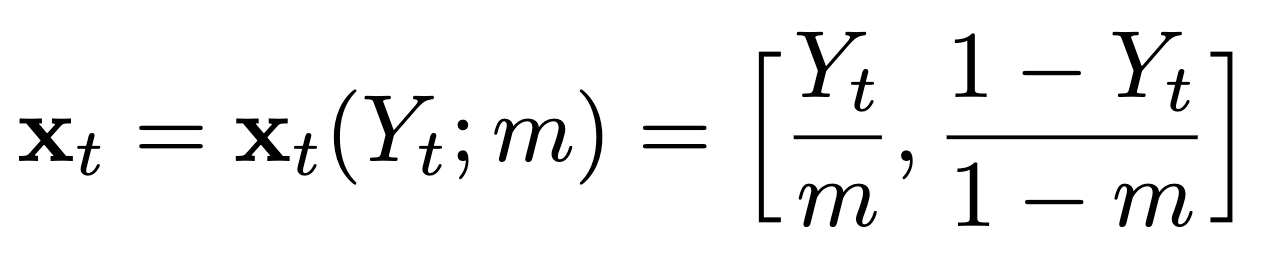overview
To apply ML techniques to scientific and engineering systems, we require reliable uncertainty estimates. Models must quantify uncertainty, detect distribution shift, and support adaptive decision making, yet many uncertainty quantification (UQ) techniques in deep learning remain ad hoc. Often, classical methods do not scale, and heuristic approaches behave unpredictably in safety-critical environments such as control, robotics, and adaptive sensing.
My work approaches UQ along two complementary fronts:
- theoretical tools for anytime-valid and sequential decision making, and
- practical diagnostics and corrections for empirical UQ methods in large models.
Many scientific and engineering tasks operate in sequential or adaptive settings where fixed-time uncertainty bounds fail. Using ideas from universal coding and gambling, I develop confidence sequences (CSs) that provide time-uniform uncertainty guarantees. These results strengthen classical concentration bounds and support sequential decision making problems such as A/B testing and contextual bandits.
This line of work establishes the power of information-theoretic constructions of confidence sequences, including:
- confidence sequences for bounded variables [1],
- confidence sequences for bounded vectors [2], and
- confidence sequences for semi-unbounded variables [3], which have applications in offline bandit problems.
diagnosing empirical UQ
There are many proposals for scalable uncertainty quantification in large neural predictive models, yet their statistical meanings and failure modes often remain unclear. In [4], we analyze evidential deep learning and show that its uncertainty targets do not correspond to the underlying data distribution, contrary to the original interpretation. This explains its inconsistent empirical behavior and highlights structural issues in commonly used heuristic UQ pipelines. These findings motivate the need for uncertainty quantification methods that remain meaningful and reliable even in large-scale or misspecified regimes.
broader perspective
These theoretical and empirical perspectives support reliable decision making in systems such as data-driven control, safe autonomy, adaptive sensing, and scientific inference. Ongoing work includes:
- extending confidence sequence techniques to operator-valued settings such as streaming PCA,
- integrating time-uniform UQ with operator learning and generative modeling,
- and designing UQ frameworks that scale to large models with provable reliability guarantees.
These tools aim to provide the foundations for uncertainty-aware scientific and engineering workflows, where reliable decisions depend on trustworthy uncertainty estimates.
references
2025
-
Improved Offline Contextual Bandits with Second-Order Bounds: Betting and Freezing
In COLT, June 2025
TL;DR: We introduce a betting-based confidence bound for off-policy selection, and a new off-policy learning technique that provides a favorable bias-variance tradeoff.
Abs arXiv PDF Code We consider off-policy selection and learning in contextual bandits, where the learner aims to select or train a reward-maximizing policy using data collected by a fixed behavior policy. Our contribution is two-fold. First, we propose a novel off-policy selection method that leverages a new betting-based confidence bound applied to an inverse propensity weight sequence. Our theoretical analysis reveals that this method achieves a significantly improved, variance-adaptive guarantee over prior work. Second, we propose a novel and generic condition on the optimization objective for off-policy learning that strikes a different balance between bias and variance. One special case, which we call freezing, tends to induce low variance, which is preferred in small-data regimes. Our analysis shows that it matches the best existing guarantees. In our empirical study, our selection method outperforms existing methods, and freezing exhibits improved performance in small-sample regimes.
2024
-
On Confidence Sequences for Bounded Random Processes via Universal Gambling Strategies
IEEE TransIT, June 2024
TL;DR: We provide a simple two-horse-race perspective for constructing confidence sequences for bounded random processes, demonstrate new properties of the confidence sequence induced by universal portfolio, and propose its computationally efficient relaxations.
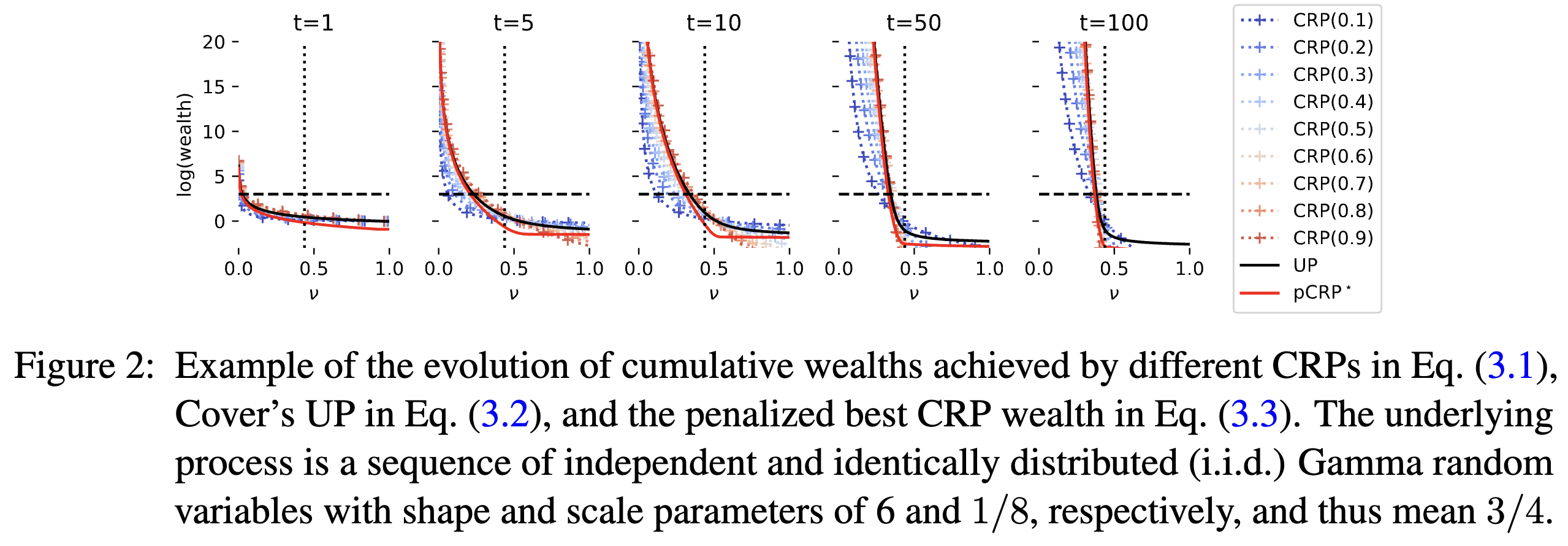
Abs arXiv HTML PDF Code This paper considers the problem of constructing a confidence sequence, which is a sequence of confidence intervals that hold uniformly over time, for estimating the mean of bounded real-valued random processes. This paper revisits the gambling-based approach established in the recent literature from a natural \emphtwo-horse race perspective, and demonstrates new properties of the resulting algorithm induced by Cover (1991)’s universal portfolio. The main result of this paper is a new algorithm based on a mixture of lower bounds, which closely approximates the performance of Cover’s universal portfolio with constant per-round time complexity. A higher-order generalization of a lower bound on a logarithmic function in (Fan et al., 2015), which is developed as a key technique for the proposed algorithm, may be of independent interest.
-
Gambling-Based Confidence Sequences for Bounded Random Vectors
In ICML, July 2024
Spotlight TL;DR: We propose a new approach to constructing confidence sequences for means of bounded multivariate stochastic processes using a general gambling framework.
Abs arXiv HTML PDF Code Poster A confidence sequence (CS) is a sequence of confidence sets that contains a target parameter of an underlying stochastic process at any time step with high probability. This paper proposes a new approach to constructing CSs for means of bounded multivariate stochastic processes using a general gambling framework, extending the recently established coin toss framework for bounded random processes. The proposed gambling framework provides a general recipe for constructing CSs for categorical and probability-vector-valued observations, as well as for general bounded multidimensional observations through a simple reduction. This paper specifically explores the use of the mixture portfolio, akin to Cover’s universal portfolio, in the proposed framework and investigates the properties of the resulting CSs. Simulations demonstrate the tightness of these confidence sequences compared to existing methods. When applied to the sampling without-replacement setting for finite categorical data, it is shown that the resulting CS based on a universal gambling strategy is provably tighter than that of the posterior-prior ratio martingale proposed by Waudby-Smith and Ramdas.
-
Are Uncertainty Quantification Capabilities of Evidential Deep Learning a Mirage?
In NeurIPS, December 2024
TL;DR: We theoretically characterize the pitfalls of evidential deep learning (EDL) in quantifying predictive uncertainty by unifying various EDL objective functions, and empirically demonstrate their failure modes.
Abs arXiv HTML PDF Code Poster Slides This paper questions the effectiveness of a modern predictive uncertainty quantification approach, called \emphevidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their perceived strong empirical performance on downstream tasks, a line of recent studies by Bengs et al. identify limitations of the existing methods to conclude their learned epistemic uncertainties are unreliable, e.g., in that they are non-vanishing even with infinite data. Building on and sharpening such analysis, we 1) provide a sharper understanding of the asymptotic behavior of a wide class of EDL methods by unifying various objective functions; 2) reveal that the EDL methods can be better interpreted as an out-of-distribution detection algorithm based on energy-based-models; and 3) conduct extensive ablation studies to better assess their empirical effectiveness with real-world datasets. Through all these analyses, we conclude that even when EDL methods are empirically effective on downstream tasks, this occurs despite their poor uncertainty quantification capabilities. Our investigation suggests that incorporating model uncertainty can help EDL methods faithfully quantify uncertainties and further improve performance on representative downstream tasks, albeit at the cost of additional computational complexity.