probabilistic and generative modeling

overview

Probabilistic and generative modeling are core components of statistical inference and modern machine learning, supporting tasks such as representation learning, scientific data modeling, and structured prediction. I develop probabilistic and generative modeling methods grounded in first principles, including divergence minimization and density-ratio estimation with statistical guarantees. The goal is to design learning objectives that are stable, interpretable, and effective in high-dimensional scientific settings, while offering a unified view of methods that are often studied separately.

Below are some recent works in this direction.

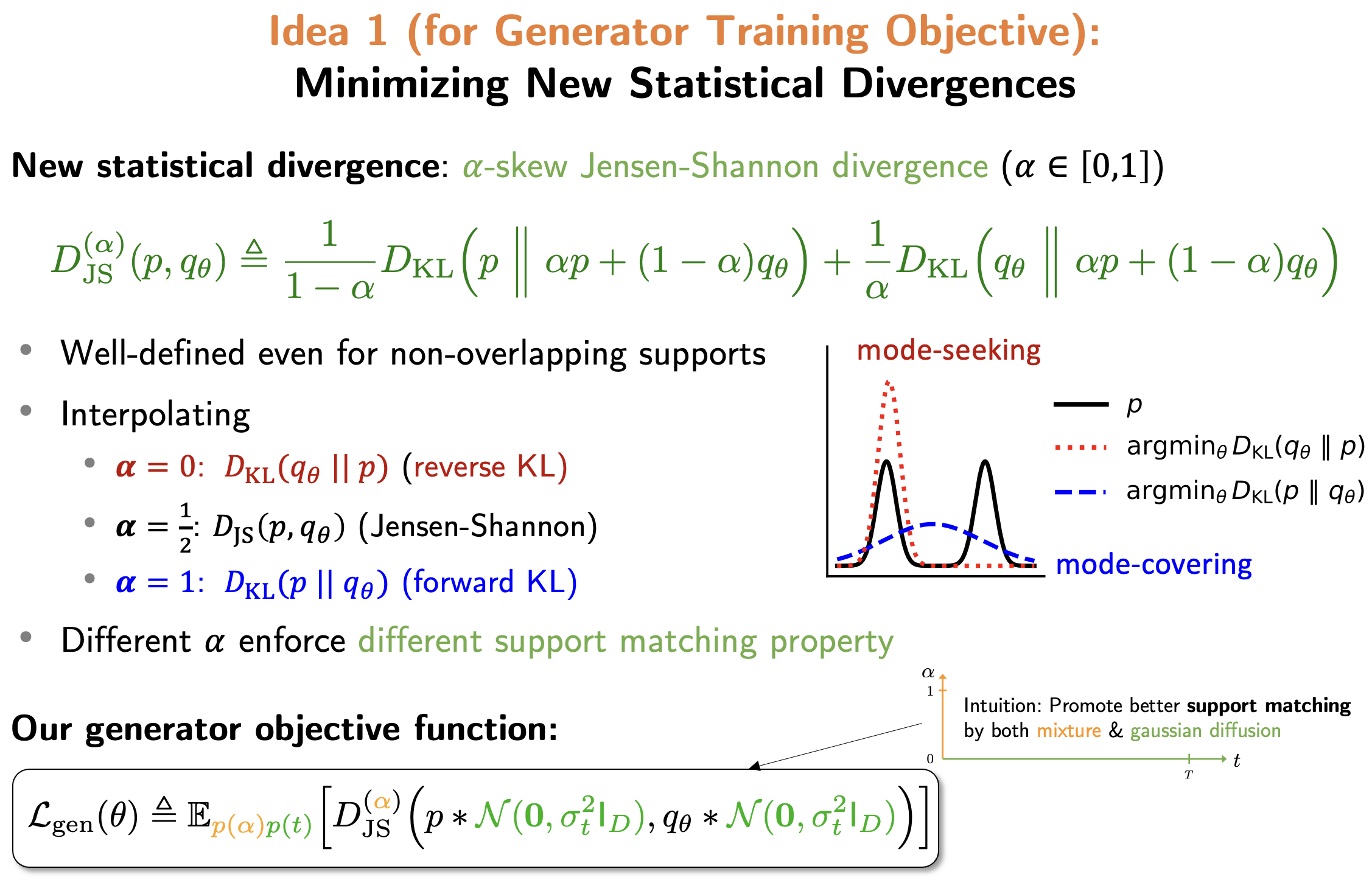
score-of-mixture training for one-step generative models [1]

Recent advances in diffusion modeling aim to reduce sampling complexity while maintaining high sample quality. In [1], we introduce the Score-of-Mixture framework, a new formulation for training one-step score-based generative models based on statistical divergence minimization. The method uses score estimation for gradient evaluation during training, and achieves stable optimization and state-of-the-art sample quality.

unifying and improving contrastive learning principles

(1) unified learning principles for energy-based models [2]

Energy-based models are expressive and broadly used in generative modeling, causal inference, and computational physics, but are difficult to train due to the unknown partition function. In [2], we provide a unified analysis of many existing estimators through noise contrastive estimation within a Bregman divergence framework. This perspective clarifies connections among methods, provides statistical consistency guarantees, and identifies common failure modes.

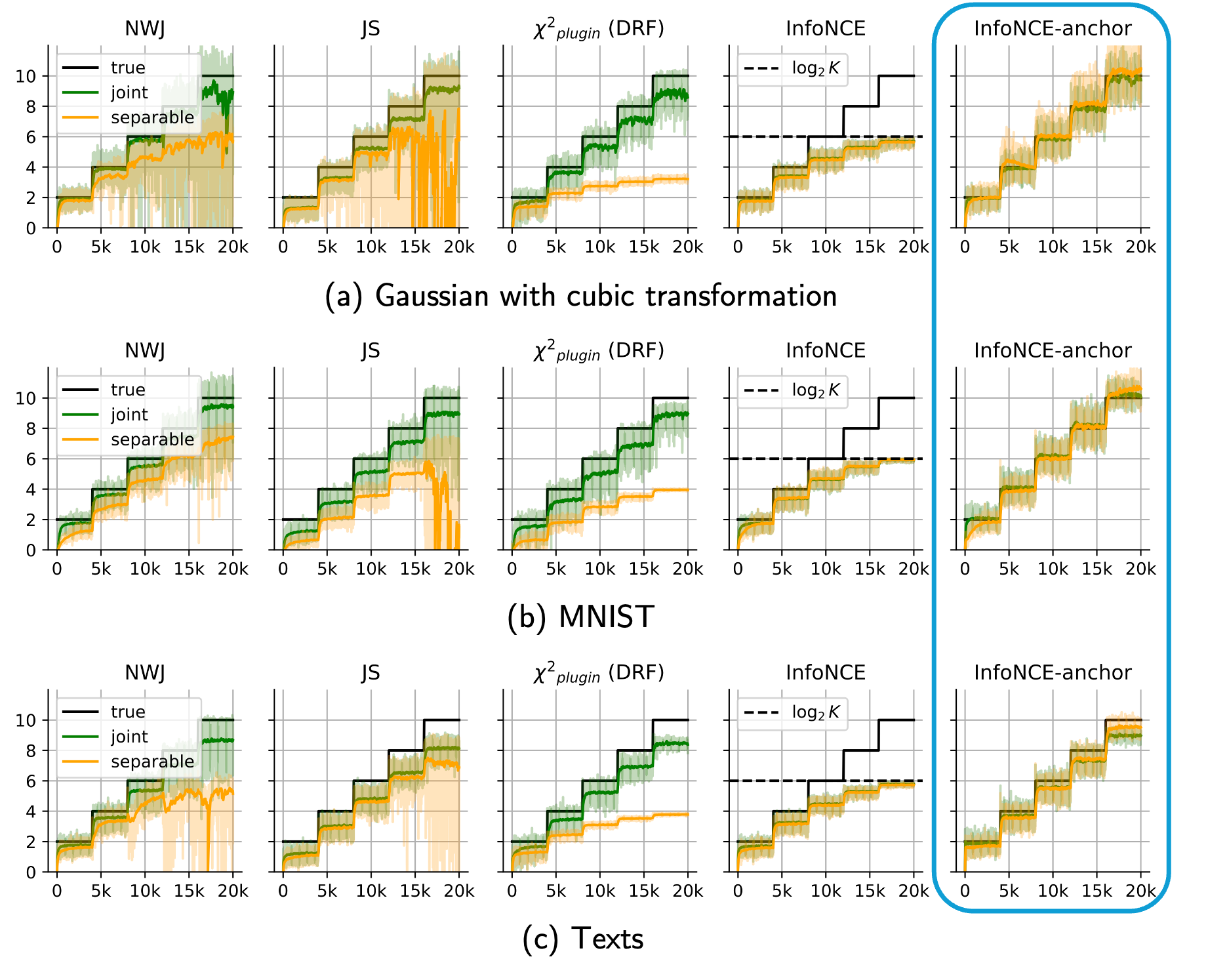
(2) consistent neural density-ratio estimation [3]

InfoNCE is widely used for representation learning, yet its relationship to mutual information has remained unclear.
In [3], we demystify the InfoNCE objective by providing the sharp information-theoretic characterization of the objective, and introduce a simple correction that resolves this issue, yielding consistent density-ratio and mutual-information estimation. This provides a principled basis for ratio-based learning across various downstream tasks in machine learning.

broader perspective

These probabilistic tools support a range of modeling tasks, including score-based generative modeling for scientific data, energy-based formulations for structured prediction, and ratio-based training for representation learning and distribution estimation.

Probabilistic and generative modeling connect modern deep learning with classical ideas in statistics, information theory, and stochastic processes. Ongoing work includes:

developing score-based models aligned with operator and spectral structure,
integrating ratio-based learning with uncertainty quantification,
and applying these methods to scientific inverse problems and simulation pipelines.

references

2025

ICML

Score-of-Mixture Training: Training One-Step Generative Models Made Simple

Tejas Jayashankar^*, J. Jon Ryu^*, and Gregory W. Wornell

In ICML, July 2025

Spotlight
TL;DR: We propose a new method for training one-step generative models by minimizing the α-skew Jensen–Shannon divergence using score-based gradient estimates.
Abs arXiv PDF Code Poster

Top 2.6% of submissions

We propose Score-of-Mixture Training (SMT), a novel framework for training one-step generative models by minimizing a class of divergences called the α-skew Jensen-Shannon divergence. At its core, SMT estimates the score of mixture distributions between real and fake samples across multiple noise levels. Similar to consistency models, our approach supports both training from scratch (SMT) and distillation using a pretrained diffusion model, which we call Score-of-Mixture Distillation (SMD). It is simple to implement, requires minimal hyperparameter tuning, and ensures stable training. Experiments on CIFAR-10 and ImageNet 64x64 show that SMT/SMD are competitive with and can even outperform existing methods.
ICML

A Unified View on Learning Unnormalized Distributions via Noise-Contrastive Estimation

J. Jon Ryu, Abhin Shah, and Gregory W. Wornell

In ICML, July 2025

TL;DR: We provide a unified perspective on various methods for learning unnormalized distributions through the lens of noise-contrastive estimation.
Abs arXiv PDF Poster

This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.
arXiv

Contrastive Predictive Coding Done Right for Mutual Information Estimation

J. Jon Ryu, Pavan Yeddanapudi, Xiangxiang Xu, and Gregory W. Wornell

October 2025

TL;DR: We show that InfoNCE is an inconsistent MI estimator, and introduce a minimal modification that enables consistent density-ratio estimation and accurate MI estimation.
Abs arXiv

The InfoNCE objective, originally introduced for contrastive representation learning, has become a popular choice for mutual information (MI) estimation, despite its indirect connection to MI. In this paper, we demonstrate why InfoNCE should not be regarded as a valid MI estimator, and we introduce a simple modification, which we refer to as InfoNCE-anchor, for accurate MI estimation. Our modification introduces an auxiliary anchor class, enabling consistent density ratio estimation and yielding a plug-in MI estimator with significantly reduced bias. Beyond this, we generalize our framework using proper scoring rules, which recover InfoNCE-anchor as a special case when the log score is employed. This formulation unifies a broad spectrum of contrastive objectives, including NCE, InfoNCE, and f-divergence variants, under a single principled framework. Empirically, we find that InfoNCE-anchor with the log score achieves the most accurate MI estimates; however, in self-supervised representation learning experiments, we find that the anchor does not improve the downstream task performance. These findings corroborate that contrastive representation learning benefits not from accurate MI estimation per se, but from the learning of structured density ratios.