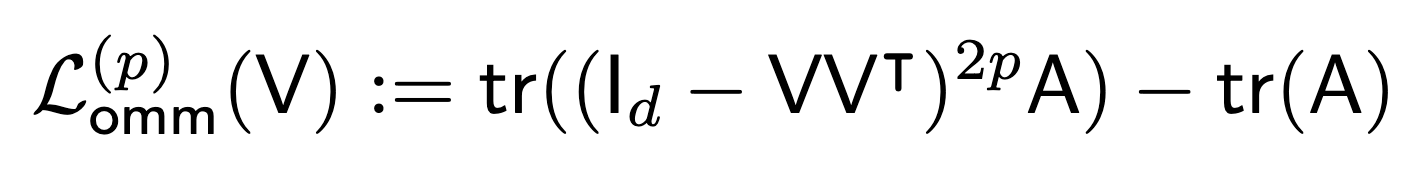neural spectral methods

overview

Neural spectral methods aim to learn the dominant spectral structure of linear operators that arise across scientific and machine learning applications, including solving PDEs, analyzing nonlinear dynamics, and learning compact representations. These methods parameterize eigenfunctions with neural networks and train them using variational principles, offering scalability and flexibility beyond classical Galerkin and finite-element approaches.

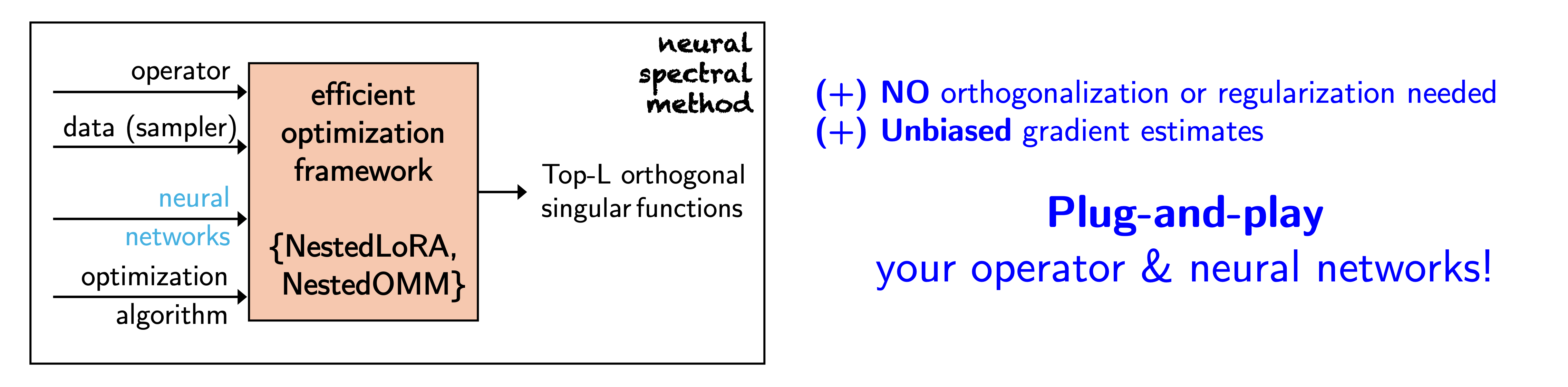
My work develops neural spectral methods through two complementary variational frameworks:

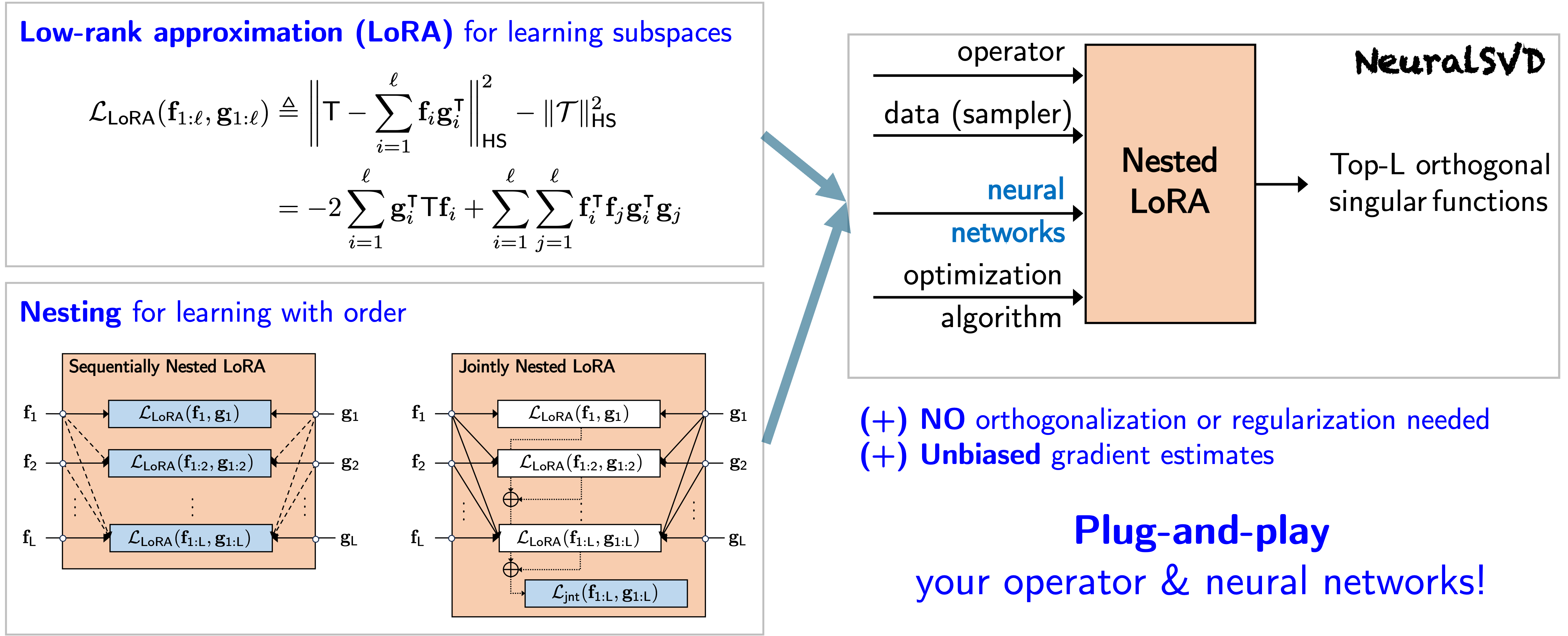
Low-rank approximation (NestedLoRA / NeuralSVD) for compact operators [1].
Orbital minimization methods (NestedOMM) for positive-semidefinite operators [2].

Both proposals use a simple nesting strategy to learn ordered eigenfunctions during training, removing the need for explicit orthogonality constraints and enabling stable optimization. These methods provide improved spectral accuracy, stronger sample efficiency, and robustness across operator learning tasks.

applications

These tools can be applied to solving PDEs as well as representation learning for reinforcement learning and graph data as demonstrated in [1] and [2].

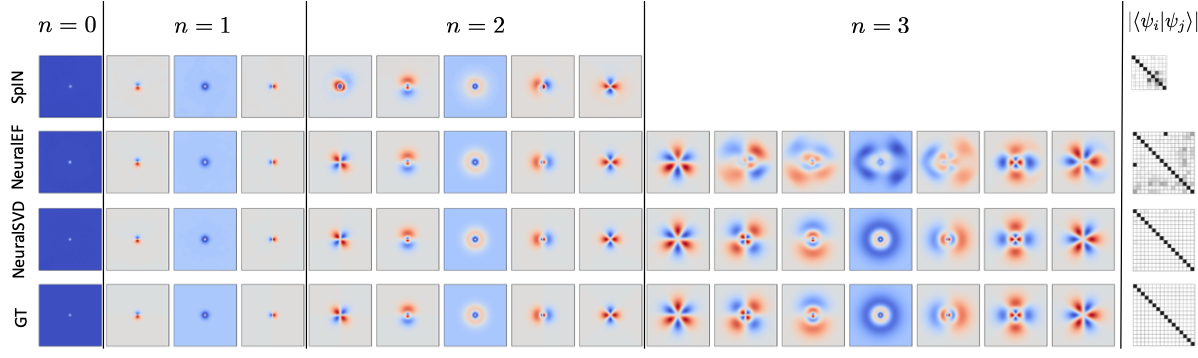
NestedLoRA learns the eigenfunctions of the Hamiltonian of the 2D hydrogen atom.

NestedLoRA can learn structured representations for complex datasets.

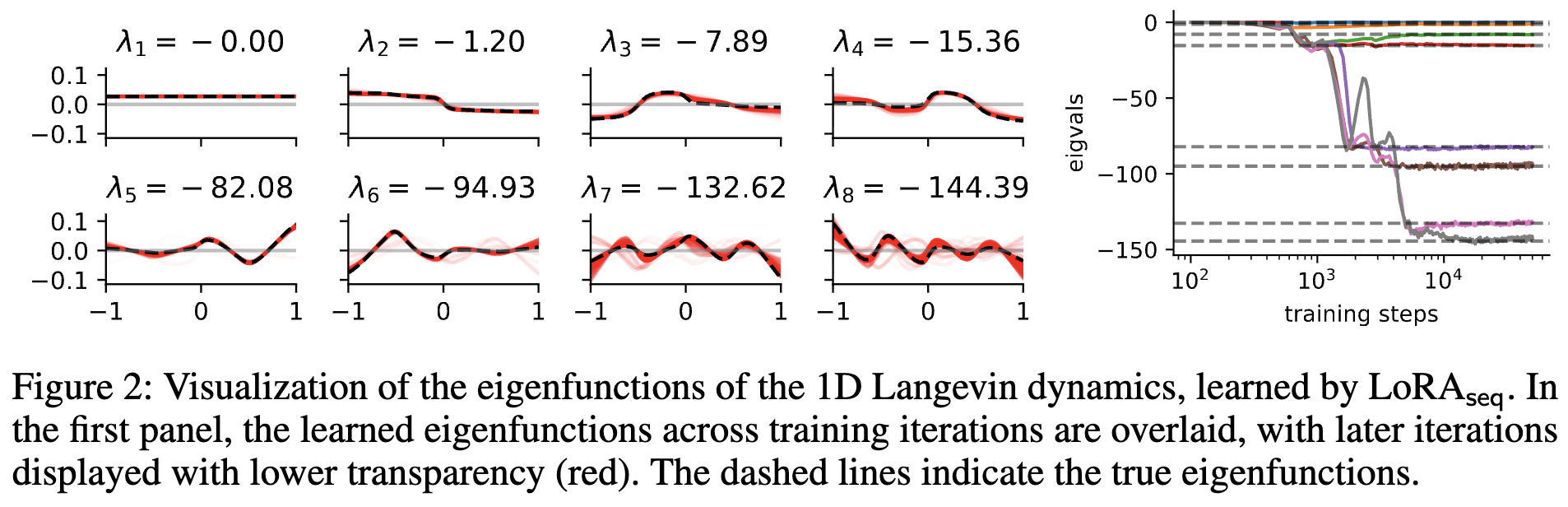
Another important application is Koopman operator learning for nonlinear dynamical systems. In [3], we demonstrate that NestedLoRA (a.k.a. NeuralSVD) learns compact Koopman approximations more accurately and efficiently than VAMPnet and DPNet, enabling better long-horizon prediction and interpretable dynamical modes.

NestedLoRA achieves improved long-horizon prediction for stochastic dynamical systems.

NestedLoRA learns eigenfunctions of continuous-time Langevin dynamics.

broader perspective

Neural spectral methods sit at the interface of operator theory, numerical linear algebra, information theory, and deep learning.
They provide a structured approach for learning operators in scientific machine learning, and open directions include:

extensions to higher-dimensional problems;
convergence analysis of neural spectral methods;
integration with uncertainty quantification;
and spectral methods for generative and inverse modeling.

references

2025

NeurIPS

Revisiting Orbital Minimization Method for Neural Operator Decomposition

J. Jon Ryu, Samuel Zhou, and Gregory W. Wornell

In NeurIPS, December 2025

TL;DR: We revisit OMM through a modern lens, developing a scalable NestedOMM formulation that trains neural networks to decompose positive semidefinite operators.
Abs arXiv HTML PDF Code

Spectral decomposition of linear operators plays a central role in many areas of machine learning and scientific computing. Recent work has explored training neural networks to approximate eigenfunctions of such operators, enabling scalable approaches to representation learning, dynamical systems, and partial differential equations (PDEs). In this paper, we revisit a classical optimization framework from the computational physics literature known as the *orbital minimization method* (OMM), originally proposed in the 1990s for solving eigenvalue problems in computational chemistry. We provide a simple linear algebraic proof of the consistency of the OMM objective, and reveal connections between this method and several ideas that have appeared independently across different domains. Our primary goal is to justify its broader applicability in modern learning pipelines. We adapt this framework to train neural networks to decompose positive semidefinite operators, and demonstrate its practical advantages across a range of benchmark tasks. Our results highlight how revisiting classical numerical methods through the lens of modern theory and computation can provide not only a principled approach for deploying neural networks in numerical analysis, but also effective and scalable tools for machine learning.
NeurIPS

Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical Systems

Minchan Jeong^*, J. Jon Ryu^*, Se-Young Yun, and Gregory W. Wornell

In NeurIPS, December 2025

TL;DR: We show that NeuralSVD (NestedLoRA) provides a scalable and stable approach for learning top-k Koopman singular functions, avoiding the unstable SVD- and inversion-based steps required by VAMPnet/DPNet.
Abs arXiv HTML PDF Code

The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.

2024

ICML

Operator SVD with Neural Networks via Nested Low-Rank Approximation

J. Jon Ryu, Xiangxiang Xu, H. S. Melichan Erol, Yuheng Bu, Lizhong Zheng, and Gregory W. Wornell

In ICML, July 2024

An extended abstract was presented at Machine Learning and the Physical Sciences Workshop, NeurIPS 2023.

TL;DR: We propose an efficient unconstrained nested optimization framework for computing the leading singular values and singular functions of a linear operator using neural networks.
Abs arXiv HTML PDF Code Poster Slides

Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-L singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.