ECE 225B: Universal Probability and Applications @UCSD¶
Homework 3: Universal portfolios¶
Due: June 4, 2018, 11:59 PM
Late homework will never be accepted.
The homework will be collected through Gradescope. Please follow the submission instruction on Piazza.
Please read the following problems carefully, and write down your code as clearly as possible and add suitable comments.
NAME:
PID:
In this homework, we will implement the Universal Portfolio algorithm by Cover.
[1] Cover, Thomas M. "Universal Portfolios." Mathematical Finance 1.1 (1991): 1-29.
[2] Blum, Avrim, and Adam Kalai. "Universal portfolios with and without transaction costs." Machine Learning 35.3 (1999): 193-205.
[3] Kalai, Adam, and Santosh Vempala. "Efficient algorithms for universal portfolios." Journal of Machine Learning Research 3.Nov (2002): 423-440.
[4] Cover, Thomas M., and Joy A. Thomas. Elements of information theory. John Wiley & Sons, 2012.
Review¶
1) Constant rebalanced portfolio as a probability induced portfolio¶
Let $m$ be the number of stocks of our interest. Recall that a probability induced portfolio gives us a "fund of funds" strategy, which is a mixture of all extremal strategies. More precisely, let $\mathrm{a}=\mathrm{a}_p$ be the portfolio induced by a pmf $p$. Then, $$ \mathrm{a}_{ij}(\mathrm{\mathbf{x}}^{i-1}) =\frac{ \displaystyle\sum_{y^{i-1}}p(j|y^{i-1})\mathrm{\mathbf{x}}(y^{i-1})p(y^{i-1}) }{ \displaystyle\sum_{y^{i-1}}p(y^{i-1})\mathrm{\mathbf{x}}(y^{i-1}) }. $$ A constant rebalanced portfolio (CRP) with $\theta=(\theta_1,\ldots,\theta_m)\in\Delta^{m-1}$ is induced by an iid probability $p_{\theta}(y^n)=\prod_{i=1}^n p_{\theta}(y_i)$, where $p_{\theta}(y)=\theta_y$ for $y\in[m]$.
2) Cover's Universal Portfolio algorithm¶
To compete with the class of CRPs, let's consider a mixture strategy. For a density $w(\theta)$ of $\theta$ over the simplex $\Delta^{m-1}$, we consider $$ q_w(y^n)=\int_{\Delta^{m-1}} p_{\theta}(y^n)w(\theta)d\theta. $$ Then, we have $$ \mathrm{b}_{ij}(\mathrm{\mathbf{x}}^{i-1}) =\frac{ \displaystyle\int \theta_j \mathbf{S}_{i-1}(\theta,\mathbf{X}^{i-1})w(\theta)d\theta }{ \displaystyle\int \mathbf{S}_{i-1}(\theta,\mathbf{X}^{i-1})w(\theta)d\theta }, $$ and further $$ \mathbf{S}_n(\mathrm{b},\mathbf{X}^n)=\int \mathbf{S}_n(\theta,\mathbf{X}^n)w(\theta)d\theta. $$ In other words, this mixture strategy is equivalent to investing your money over the simplex continuously according to the weight $w(\theta)$. In particular, Cover's Universal Portfolio ($\mathsf{UP}$) algorithm is using $\mathsf{Dirichlet}(1/2,\ldots,1/2)$ prior for the density (or weight) $w(\theta)$. In general, let's call $\mathsf{UP}(\alpha)$ algorithm for the mixture startegy with $\mathsf{Dirichlet}(\alpha,\ldots,\alpha)$ prior.
3) Implementation¶
Note that, however, the exact integration is computationally difficult. Hence, in this homework, we approximate the integration by Monte-Carlo sampling as follows. $$ \mathbf{S}_n(\mathrm{b},\mathbf{X}^n)\approx \frac{1}{N}\sum_{k=1}^N \mathbf{S}_n(\theta_k,\mathbf{X}^n). $$
- For $N$ sufficiently large, draw $N$ probability vectors $\theta(1),\ldots,\theta(N)\in\Delta^{m-1}$, each of which corresponds to a CRP, according to the Dirichlet prior.
- Divide your money equally to those CRPs, and hold.
import numpy as np
import pandas as pd # pandas data frame
import os # to access the file directories
import matplotlib.pyplot as plt
%matplotlib inline
%pylab inline
pylab.rcParams['figure.figsize'] = (15, 6)
font = {'family' : 'serif',
'weight' : 'normal',
'size' : 12}
matplotlib.rc('font', **font)
Populating the interactive namespace from numpy and matplotlib
The stock data¶
In data/ folder, we provide a historical data over 10 years from Jan-01-17 to Dec-31-18 of 10 stocks having index of a single symbol. The data was collected at Yahoo! Finance (https://finance.yahoo.com/).
You are more than welcome to download any other stock you are interested in for this homework.
stock_name_dict = {'A': 'Agilent Technologies, Inc.',
'B': 'Barnes Group Inc.',
'C': 'Citigroup Inc.',
'D': 'Dominion Energy, Inc.',
'F': 'Ford Motor Company',
'M': 'Macy\'s, Inc.',
'S': 'Sprint Corporation',
'T': 'AT&T Inc.',
'X': 'United States Steel Corporation',
'Y': 'Alleghany Corporation'}
The following code preprocesses the historical data.
directory = 'data/'
stocks_dict = {}
prices_dict = {}
price_relatives_dict = {}
for filename in os.listdir(directory):
if filename.endswith(".csv"):
df = pd.read_csv(directory+filename)
stock_symbol = os.path.splitext(filename)[0]
temp_dict = {}
temp_dict['Name'] = stock_name_dict[stock_symbol]
temp_dict['Close'] = np.array(df['Close'])
temp_dict['Relative'] = np.array(df['Close']/df['Open'])
stocks_dict[stock_symbol] = temp_dict
else:
continue
for key in stocks_dict:
plt.plot(stocks_dict[key]['Close'], label=stocks_dict[key]['Name'])
plt.legend(loc=1)
plt.title(r'Stock prices');
plt.figure()
for key in stocks_dict:
plt.plot(stocks_dict[key]['Relative'], label=stocks_dict[key]['Name'])
plt.legend(loc=1)
plt.title(r'Price relatives');
prices_stack = np.vstack([stocks_dict[k]['Close'] for k in stocks_dict])
price_relatives_stack = np.vstack([stocks_dict[k]['Relative'] for k in stocks_dict])
Problem 1. (Approximate optimal CRP in hindsight)¶
In this problem, we find the optimal CRP in hindsight given the price relatives. Again, as the exact optimization is hard, we will perform a Monte Carlo search by sampling random points uniformly over the simplex. (It is okay to implement a grid search if you wish.)
Write a function
approx_optimal_CRP(price_relatives_stack, N)
which takes price_relatives_stack and N the number of random samples as inputs,
and outputs
- the optimal CRP (i.e., the optimal probability vector), and
- the optimal wealth achieved by the CRP.
Hint: The $\mathsf{Dirichlet}(1,\ldots,1)$ is the uniform distribution over the simplex, and np.random.dirichlet generates a Dirichlet random vector.
By the way, can you sample a point uniformly at random from the simplex without using the predifined Dirichlet sampling?
def approx_optimal_CRP(price_relatives_stack, N):
### FILL IN YOUR CODE ###
return
Problem 2. (Approximate Universal Portfolio algorithm)¶
In this problem, we implemet the approximate Universal Portfolio algorithm $\mathsf{UP}(\alpha)$.
Write a function
approx_UP(price_relatives_stack, N, alpha)
that takes
price_relatives_stack,alphathe parameter for the $\mathsf{Dirichlet}$ prior, andNthe number of random samples drawn from the $\mathsf{Dirichlet}(\alpha,\ldots,\alpha)$ prior
as inputs, and outputs
- the wealth ratio achieved by the UP.
def approx_UP(price_relatives_stack, alpha=1/2, N=100):
### FILL IN YOUR CODE ###
return
Problem 3. (Experiments)¶
Now based on our the implementations, we would like to check the performance of the $\mathsf{UP}$ algorithm compared to the optimal CRP using the real market data.
As mentioned at the beginning, you can download additional data to perform the following experiments.
Problem 3(a).¶
Choose any two stocks such that the performance of the CRP over the stocks looks as follows.
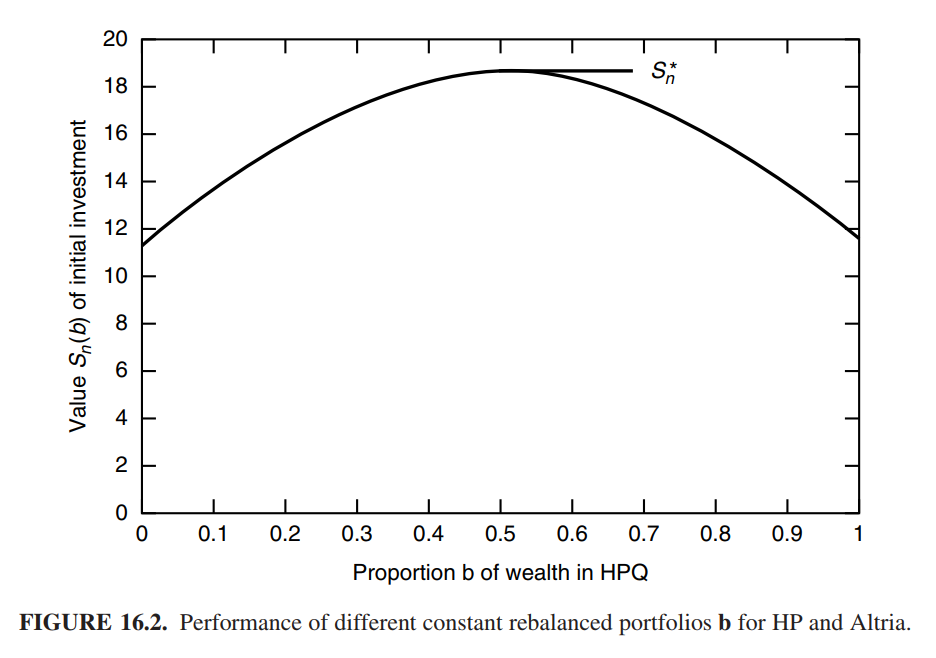 |
Draw the same plot for the selected stocks, and draw horizontal lines of the performance of the UP algorithm for $\alpha\in\{0.1,0.2,\ldots,1\}$.
Problem 3(b).¶
Repeat the previous experiment with three, four, and five stocks. For these high-dimensional problems, you do not have to plot the performance of the CRPs. Make some comments on your results. Do you think you would invest your money using the Universal Portfolio algorithm?
NOTE: Please ensure that you are using $N$ large enough to find a good approximate for the optimal values. To see the qunatitative guarantee for the Monte Carlo approximation, see [2].
### FILL IN YOUR CODE ###